题目内容
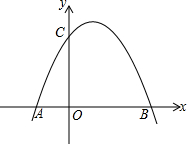
如图,抛物线y=x2-2x+k与x轴交于A、B两点,与y轴交于点C(0,-3).
(1)k=______,点A的坐标为______,点B的坐标为______;
(2)设抛物线y=x2-2x+k的顶点为M,求四边形ABMC的面积;
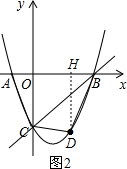
(3)在直线BC下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由;
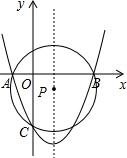
(4)设经过点A、B、C三点的圆是⊙P,请直接写出:它的半径长为______,圆心P的坐标为______.

(1)k=______,点A的坐标为______,点B的坐标为______;
(2)设抛物线y=x2-2x+k的顶点为M,求四边形ABMC的面积;
(3)在直线BC下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由;
(4)设经过点A、B、C三点的圆是⊙P,请直接写出:它的半径长为______,圆心P的坐标为______.

(1)∵抛物线y=x2-2x+k经过点C(0,-3),
∴k=-3,
∴抛物线的解析式为:y=x2-2x-3,当y=0时,
∴x2-2x-3=0,解得:
x1=-1,x2=3,
∴A(-1,0),B(3,0)
故答案为:-3,(-1,0),(3,0)
(2)∵y=x2-2x-3,
∴y=(x-1)2-4,
∴M(1,-4),作MG⊥x轴,
∴MG=4,OG=1.
∵A(-1,0),C(0,-3),B(3,0),
∴OA=1,OC=3,GB=2,
∴S四边形ABMC=S△AOC+S四边形OCMG+S△GMB,
=
+
+
=5+4
=9
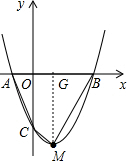
(3)设D(x,x2-2x-3),
∴OH=x,DH=2x+3-x2,HB=3-x
∴S四边形ABDC=S△AOC+S四边形OCDH+S△HDB,
=
+
+
=-
(x-
)2+
∴x=
时,S四边形ABDC的最大值为
,
∴y=
-3-3=-
,
∴D(
,-
)
(4)P(1,-1),⊙P的半径为:
∴k=-3,
∴抛物线的解析式为:y=x2-2x-3,当y=0时,
∴x2-2x-3=0,解得:
x1=-1,x2=3,
∴A(-1,0),B(3,0)
故答案为:-3,(-1,0),(3,0)
(2)∵y=x2-2x-3,
∴y=(x-1)2-4,
∴M(1,-4),作MG⊥x轴,
∴MG=4,OG=1.
∵A(-1,0),C(0,-3),B(3,0),
∴OA=1,OC=3,GB=2,
∴S四边形ABMC=S△AOC+S四边形OCMG+S△GMB,
=
| 1×3 |
| 2 |
| (3+4)×1 |
| 2 |
| 4×2 |
| 2 |
=5+4
=9

(3)设D(x,x2-2x-3),
∴OH=x,DH=2x+3-x2,HB=3-x
∴S四边形ABDC=S△AOC+S四边形OCDH+S△HDB,
=
| 3 |
| 2 |
| (3+2x+3-x2)x |
| 2 |
| (3-x)(2x+3-x2) |
| 2 |
=-
| 3 |
| 2 |
| 3 |
| 2 |
| 75 |
| 8 |
∴x=
| 3 |
| 2 |
| 75 |
| 8 |
∴y=
| 9 |
| 4 |
| 15 |
| 4 |
∴D(
| 3 |
| 2 |
| 15 |
| 4 |

(4)P(1,-1),⊙P的半径为:
| 5 |


练习册系列答案
相关题目