题目内容
如图,直线y= x与双曲线y=
x与双曲线y= 相交于A、B两点,BC⊥x轴于点C(﹣4,0).
相交于A、B两点,BC⊥x轴于点C(﹣4,0).

(1)求A、B两点的坐标及双曲线的解析式;
(2)若经过点A的直线与x轴的正半轴交于点D,与y轴的正半轴交于点E,且△AOE的面积为10,求CD的长.
 x与双曲线y=
x与双曲线y= 相交于A、B两点,BC⊥x轴于点C(﹣4,0).
相交于A、B两点,BC⊥x轴于点C(﹣4,0).
(1)求A、B两点的坐标及双曲线的解析式;
(2)若经过点A的直线与x轴的正半轴交于点D,与y轴的正半轴交于点E,且△AOE的面积为10,求CD的长.
(1)y= (2)9
(2)9
 (2)9
(2)9试题分析:(1)求出B的横坐标,代入y=
 x求出y,即可得出B的坐标,把B的坐标代入y=
x求出y,即可得出B的坐标,把B的坐标代入y= 求出y=
求出y= ,解方程组
,解方程组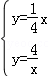 即可得出A的坐标;
即可得出A的坐标;(2)设OE=x,OD=y,由三角形的面积公式得出
 xy﹣
xy﹣ y•1=10,
y•1=10,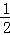 x•4=10,求出x、y,即可得出OD=5,求出OC,相加即可.
x•4=10,求出x、y,即可得出OD=5,求出OC,相加即可.解:(1)∵BC⊥x,C(﹣4,0),
∴B的横坐标是﹣4,代入y=
 x得:y=﹣1,
x得:y=﹣1,∴B的坐标是(﹣4,﹣1),
∵把B的坐标代入y=
 得:k=4,
得:k=4,∴y=
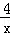 ,
,∵解方程组
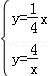 得:
得: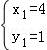 ,
,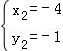 ,
,∴A的坐标是(4,1),
即A(4,1),B(﹣4,﹣1),反比例函数的解析式是y=
 .
.(2)设OE=x,OD=y,
由三角形的面积公式得:
 xy﹣
xy﹣ y•1=10,
y•1=10, x•4=10,
x•4=10,解得:x=5,y=5,
即OD=5,
∵OC=|﹣4|=4,
∴CD的值是4+5=9.
点评:本题考查了三角形的面积、一次和与反比例函数的交点问题的应用,题目比较好,但是一道比较容易出错的题目.

练习册系列答案
相关题目
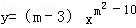 是反比例函数.
是反比例函数. 是反比例函数,则k必须满足( )
是反比例函数,则k必须满足( ) (x>0)上有一点A(1,5),过点A的直线y=mx+n与x轴交于点C(6,0).
(x>0)上有一点A(1,5),过点A的直线y=mx+n与x轴交于点C(6,0).
 的图象,则关于x的方程
的图象,则关于x的方程 的图象在第二、第四象限,那么m可能取的一个值为
的图象在第二、第四象限,那么m可能取的一个值为 ,k<0的图象上有两点(-1,y1),(-
,k<0的图象上有两点(-1,y1),(- ,y2),
,y2), x+2与坐标轴交于A、B两点,与双曲线y=
x+2与坐标轴交于A、B两点,与双曲线y= 交于点C,A、D关于y轴对称,若S四边形OBCD=6,则k= .
交于点C,A、D关于y轴对称,若S四边形OBCD=6,则k= .
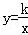 (k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若
(k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若 (m为大于l的常数).记△CEF的面积为S1,△OEF的面积为S2,则
(m为大于l的常数).记△CEF的面积为S1,△OEF的面积为S2,则 = . (用含m的代数式表示)
= . (用含m的代数式表示)