题目内容
如图,在平面直角坐标系xOy中,直线AB与x轴、y轴分别交于点A,B,与反比例函数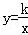 (k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若
(k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若 (m为大于l的常数).记△CEF的面积为S1,△OEF的面积为S2,则
(m为大于l的常数).记△CEF的面积为S1,△OEF的面积为S2,则 = . (用含m的代数式表示)
= . (用含m的代数式表示)
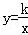 (k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若
(k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若 (m为大于l的常数).记△CEF的面积为S1,△OEF的面积为S2,则
(m为大于l的常数).记△CEF的面积为S1,△OEF的面积为S2,则 = . (用含m的代数式表示)
= . (用含m的代数式表示)

试题分析:根据E,F都在反比例函数的图象上得出假设出E,F的坐标,进而得出△CEF的面积S1以及△OEF的面积S2,进而比较即可得出答案.
解:过点F作FD⊥BO于点D,EW⊥AO于点W,
∵
 ,
,∴
 =
= ,
,∵ME•EW=FN•DF,
∴
 =
= ,
,∴
 =
= ,
,设E点坐标为:(x,my),则F点坐标为:(mx,y),
∴△CEF的面积为:S1=
 (mx﹣x)(my﹣y)=
(mx﹣x)(my﹣y)= (m﹣1)2xy,
(m﹣1)2xy,∵△OEF的面积为:S2=S矩形CNOM﹣S1﹣S△MEO﹣S△FON,
=MC•CN﹣
 (m﹣1)2xy﹣
(m﹣1)2xy﹣ ME•MO﹣
ME•MO﹣ FN•NO,
FN•NO,=mx•my﹣
 (m﹣1)2xy﹣
(m﹣1)2xy﹣ x•my﹣
x•my﹣ y•mx,
y•mx,=m2xy﹣
 (m﹣1)2xy﹣mxy,
(m﹣1)2xy﹣mxy,=
 (m2﹣1)xy,
(m2﹣1)xy,=
 (m+1)(m﹣1)xy,
(m+1)(m﹣1)xy,∴
 =
= =
= .
.故答案为:
 .
.
点评:此题主要考查了反比例函数的综合应用以及三角形面积求法,根据已知表示出E,F的点坐标是解题关键.

练习册系列答案
相关题目
 x与双曲线y=
x与双曲线y= 相交于A、B两点,BC⊥x轴于点C(﹣4,0).
相交于A、B两点,BC⊥x轴于点C(﹣4,0).
 上,B、D在双曲线y2=
上,B、D在双曲线y2=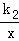 上,k1=2k2(k1>0),AB∥y轴,S?ABCD=24,则k1= .
上,k1=2k2(k1>0),AB∥y轴,S?ABCD=24,则k1= .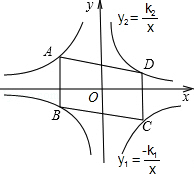
 (x<0)的图象于B,交函数
(x<0)的图象于B,交函数 (x>0)的图象于C,则线段AB与线段AC的长度之比为 _________ .
(x>0)的图象于C,则线段AB与线段AC的长度之比为 _________ .
 ;
; .
.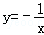 的图象上,则用“>”连接y1、y2、y3得 .
的图象上,则用“>”连接y1、y2、y3得 . 在第一象限内图象上的点,作MB⊥x轴于B.过点M的第一条直线交y轴于点A1,交反比例函数图象于点C1,且A1C1=
在第一象限内图象上的点,作MB⊥x轴于B.过点M的第一条直线交y轴于点A1,交反比例函数图象于点C1,且A1C1=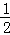 A1M,△A1C1B的面积记为S1;过点M的第二条直线交y轴于点A2,交反比例函数图象于点C2,且A2C2=
A1M,△A1C1B的面积记为S1;过点M的第二条直线交y轴于点A2,交反比例函数图象于点C2,且A2C2=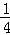 A2M,△A2C2B的面积记为S2;过点M的第三条直线交y轴于点A3,交反比例函数图象于点C3,且A3C3=
A2M,△A2C2B的面积记为S2;过点M的第三条直线交y轴于点A3,交反比例函数图象于点C3,且A3C3=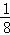 A3M,△A3C3B的面积记为S3;以此类推…;则S1+S2+S3+…+S8= _________ .
A3M,△A3C3B的面积记为S3;以此类推…;则S1+S2+S3+…+S8= _________ .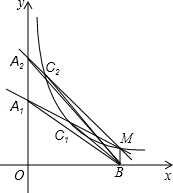
 (x>0)的图象上时,设△ABC在第一象限部分的面积分别记做S1、S2(如图1、图2所示)D是斜边与y轴的交点,通过计算比较S1、S2的大小.
(x>0)的图象上时,设△ABC在第一象限部分的面积分别记做S1、S2(如图1、图2所示)D是斜边与y轴的交点,通过计算比较S1、S2的大小.
 和
和 的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为( )
的图象分别是l1和l2.设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则三角形PAB的面积为( )
