题目内容
如图,已知直线y= x+2与坐标轴交于A、B两点,与双曲线y=
x+2与坐标轴交于A、B两点,与双曲线y= 交于点C,A、D关于y轴对称,若S四边形OBCD=6,则k= .
交于点C,A、D关于y轴对称,若S四边形OBCD=6,则k= .
 x+2与坐标轴交于A、B两点,与双曲线y=
x+2与坐标轴交于A、B两点,与双曲线y= 交于点C,A、D关于y轴对称,若S四边形OBCD=6,则k= .
交于点C,A、D关于y轴对称,若S四边形OBCD=6,则k= .

试题分析:求出A、B的坐标,求出D的坐标,求出AD、OB的值,设C的坐标是(x,
 x+2),根据已知得出S△ACD﹣S△AOB=6,推出
x+2),根据已知得出S△ACD﹣S△AOB=6,推出 ×(4+4)×(
×(4+4)×(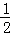 x+2)﹣
x+2)﹣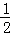 ×4×2=6,求出C的坐标即可.
×4×2=6,求出C的坐标即可.解:∵y=
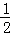 x+2,
x+2,∴当x=0时,y=2,
当y=0时,0=
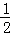 x+2,
x+2,x=﹣4,
即A(﹣4,0),B(0,2),
∵A、D关于y轴对称,
∴D(4,0),
∵C在y=
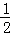 x+2上,
x+2上,∴设C的坐标是(x,
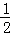 x+2),
x+2),∵S四边形OBCD=6,
∴S△ACD﹣S△AOB=6,
∴
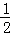 ×(4+4)×(
×(4+4)×(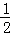 x+2)﹣
x+2)﹣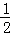 ×4×2=6,
×4×2=6,x=1,
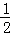 x+2=
x+2= ,
,C(1,
 ),
),代入y=
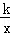 得:k=
得:k= .
.故答案为:
 .
.点评:本题考查了一次函数与反比例函数的交点问题,三角形的面积等知识点,主要考查学生的计算能力,题目具有一定的代表性,是一道比较好的题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 x与双曲线y=
x与双曲线y= 相交于A、B两点,BC⊥x轴于点C(﹣4,0).
相交于A、B两点,BC⊥x轴于点C(﹣4,0).
 的图象相交于A,B两点,已知A(1,4).
的图象相交于A,B两点,已知A(1,4).
 的解集.
的解集. 上,B、D在双曲线y2=
上,B、D在双曲线y2=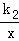 上,k1=2k2(k1>0),AB∥y轴,S?ABCD=24,则k1= .
上,k1=2k2(k1>0),AB∥y轴,S?ABCD=24,则k1= .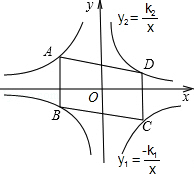
 (x<0)的图象于B,交函数
(x<0)的图象于B,交函数 (x>0)的图象于C,则线段AB与线段AC的长度之比为 _________ .
(x>0)的图象于C,则线段AB与线段AC的长度之比为 _________ .
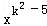 是反比例函数,则k= .
是反比例函数,则k= . (x>0)的图象上时,设△ABC在第一象限部分的面积分别记做S1、S2(如图1、图2所示)D是斜边与y轴的交点,通过计算比较S1、S2的大小.
(x>0)的图象上时,设△ABC在第一象限部分的面积分别记做S1、S2(如图1、图2所示)D是斜边与y轴的交点,通过计算比较S1、S2的大小.
 的对称性叙述错误的是( )
的对称性叙述错误的是( )