题目内容
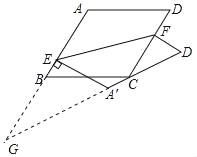
【题目】如图,折叠菱形纸片ABCD,使得A′D′对应边过点C,若∠B=60°,AB=2,当A′E⊥AB时,AE的长是( )

A.2![]() B.2
B.2![]() C.
C.![]() D.1+
D.1+![]()
【答案】B
【解析】
先延长AB,D'A'交于点G,根据三角形外角性质以及等腰三角形的判定,即可得到BC=BG=BA,设AE=x=A'E,则BE=2x,GE=4x,A'G=2x,在Rt△A'GE中,依据勾股定理可得A'E2+GE2=A'G2,进而得出方程,解方程即可.
解:如图所示,延长AB,D'A'交于点G,
∵A'E⊥AB,∠EA'C=∠A=120°,
∴∠BGC=120°﹣90°=30°,
又∵∠ABC=60°,
∴∠BCG=60°﹣30°=30°,
∴∠BGC=∠BCG=30°,
∴BC=BG=BA,
设AE=x=A'E,则BE=AB﹣AE=2﹣x,A'G=2x,
∴GE=BG+BE=2+2﹣x=4﹣x,
∵Rt△A'GE中,A'E2+GE2=A'G2,
∴x2+(4﹣x)2=(2x)2,
解得:x=﹣2+2![]() ,(负值已舍去)
,(负值已舍去)
∴AE=2![]() ﹣2,
﹣2,
故选:B.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目