题目内容
【题目】某地图书馆为了满足群众多样化阅读的需求,决定购买甲、乙两种品牌的电脑若干组建电子阅览室.经了解,甲、乙两种品牌的电脑单价分别3100元和4600元.
(1)若购买甲、乙两种品牌的电脑共50台,恰好支出200000元,求甲、乙两种品牌的电脑各购买了多少台?
(2)若购买甲、乙两种品牌的电脑共50台,每种品牌至少购买一台,且支出不超过160000元,共有几种购买方案?并说明哪种方案最省钱.
【答案】(1)甲种品牌的电脑购买了20台,乙种品牌的电脑购买了30台;(2)一共有三种购买方案,甲种品牌的电脑购买49台,乙种品牌的电脑购买1台比较省钱.
【解析】分析:(1)设甲种品牌的电脑购买了x台,乙种品牌的电脑购买了y台,根据题意建立二元一次方程组,求出其解即可;
(2)设甲种品牌的电脑购买了x台,乙种品牌的电脑购买了(50-x)台,根据题意建立不等式组求出其解即可.
详解:(1)设甲种品牌的电脑购买了x台,乙种品牌的电脑购买了y台,则
![]() ,
,
解得![]() ,
,
答:甲种品牌的电脑购买了20台,乙种品牌的电脑购买了30台.
(2)设甲种品牌的电脑购买了x台,乙种品牌的电脑购买了(50-x)台,则
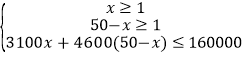 ,
,
解得![]() ≤x≤49,
≤x≤49,
∴x的整数值为47,48、49,
当x=47时,50-x=3;当x=48时,50-x=2;当x=49时,50-x=1.
∴一共有三种购买方案:甲种品牌的电脑购买47台,乙种品牌的电脑购买3台;甲种品牌的电脑购买48台,乙种品牌的电脑购买2台;甲种品牌的电脑购买49台,乙种品牌的电脑购买1台.
∵甲、乙两种品牌的电脑单价分别3100元和4600元.
∴甲种品牌的电脑购买49台,乙种品牌的电脑购买1台比较省钱.

练习册系列答案
相关题目