题目内容
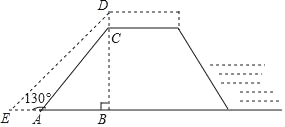
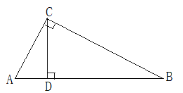
【题目】如图,ΔABC中,AB=AC,∠A=40O,延长AC到D,使CD=BC,点P是ΔABD的内心,则∠BPC=

A. 105° B. 110° C. 130° D. 145°
【答案】D
【解析】
试题已知P为△ABD的内心,则P点必在∠BAC的角平分线上,由于AB=AC,根据等腰三角形的性质可知:P点必在BC的垂直平分线上,即BP=PC,△BPC也是等腰三角形,欲求∠BPC,必先求出∠PBC的度数.等腰△ABC中,已知了顶角∠A的度数,可求得∠ABC、∠ACB的度数;由于CB=CD,∠ACB是△ABC的外角,由此可求出∠D和∠CBD的度数;由于P是△ABD的内心,则PB平分∠ABD,由此可求得∠PBD的度数,根据∠PBC=∠PBD-∠CBD可求出∠PBC的度数,由此得解.
试题解析:△ABC中,AB=AC,∠A=40°;
∴∠ABC=∠ACB=70°;
∵P是△ABD的内心,
∴P点必在等腰△ABC底边BC的垂直平分线上,
∴PB=PC,∠BPC=180°-2∠PBC;
在△CBD中,CB=CD,
∴∠CBD=∠D=![]() ∠ACB=35°;
∠ACB=35°;
∵P是△ABD的内心,
∴PB平分∠ABD,
∴∠PBD=![]() ∠ABD=
∠ABD=![]() (∠ABC+∠CBD)=52.5°,
(∠ABC+∠CBD)=52.5°,
∴∠PBC=∠PBD-∠CBD=52.5°-35°=17.5°;
∴∠BPC=180°-2∠PBC=145°.
故选D.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目