Question

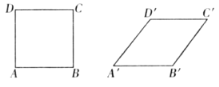
【题目】如图，只改变正方形的形状，得到四边形，且，则四边形与正方形的面积的比是（ 　）

A.1:1B.2:3C.:2D.3:4

Answer 1

【答案】C

【解析】

过点D'作D'E⊥A'B'，设正方形的边长为a，先证四边形为菱形，再利用求得D'E的长，进而求得菱形面积，再求与正方形面积之比即可．

解：如图，过点D'作D 'E⊥A ' B '，垂足为点E，

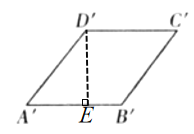
设正方形的边长为a，

则AB＝BC＝CD＝DA＝a，

∴A'B'＝B'C'＝C'D'＝D'A'＝a，

∴四边形为菱形，

∵D 'E⊥A ' B '，

∴∠A'ED'＝90°，

在Rt△A'D'E中，sin∠D'A'E＝，∠D'A'E＝60°，

∴sin60°，

∴D'E＝，

∴S菱形，

又∵S正方形＝a2，

∴S菱形：S正方形＝：a2＝．

故选：C．