题目内容
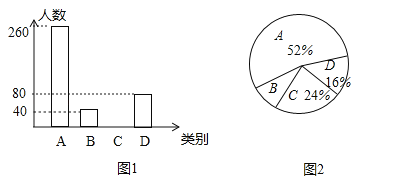
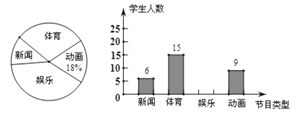
【题目】某中学为了解学生对新闻,体育,娱乐,动画四类电视节目的喜爱情况,进行了统计调查.随机调查了某班所有同学最喜欢的节目(每名学生必选且只能选择四类节目中的一类),并将调查结果绘成如下不完整的统计图.
根据两图提供的信息,回答下列问题:
(1)本次调查了多少人?
(2)请补全条形统计图;
(3)根据抽样调查结果,若该校有1000名学生,请你估计该校有多少名学生最喜欢“新闻”类节目;
(4)在全班同学中,甲,乙,丙,丁等同学最喜欢体育类节,班主任打算从甲,乙,丙,丁4名同学中选取2人参加学校组织的体育知识竞赛,请用列表法或树状图求同时选中甲,乙两同学的概率.
【答案】(1)50人;(2)作图见解析;(3)120人;(4)![]() .
.
【解析】
(1)根据最喜欢动画类节目的扇形统计图和条形统计图即可得;
(2)先根据题(1)的结论、条形统计图求出最喜欢娱乐类节目的人数,然后补全图形即可;
(3)先求出最喜欢新闻类节目的学生占比,再乘以1000即可得;
(4)先画出树状图,再找出同时选中甲、乙两同学的所有可能的结果,然后根据概率公式计算即可.
(1)由最喜欢动画类节目的扇形统计图和条形统计图得![]() (人)
(人)
答:本次调查了50人;
(2)最喜欢娱乐类节目的人数为![]() (人)
(人)
补全条形统计图如下:

(3)最喜欢新闻类节目的学生占比![]()
则估计该校最喜欢新闻类节目的学生人数为![]() (人)
(人)
答:该校有120名学生最喜欢“新闻”类节目;
(4)依题意,画树状图如下:
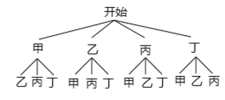
由此可知,共有12种等可能的结果,恰好同时选中甲、乙两位同学的结果有2种
则恰好同时选中甲、乙两位同学的概率为![]() .
.

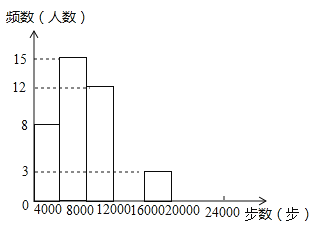
【题目】焦作市教育局为调查全市教师的运动情况,结合现今流行的“微信运动”,随机调查了本市![]() 名老师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表:
名老师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表:
步数 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
请根据以上信息,解答下列问题:
(1)写出![]() 的值,并补全频数分布直方图;
的值,并补全频数分布直方图;
(2)本市约有![]() 名教师,结合调查的数据估计日行走步数超过
名教师,结合调查的数据估计日行走步数超过![]() 步(包含
步(包含![]() 步)的教师有多少名?
步)的教师有多少名?
(3)若在被调查的教师中,选取日行走步数超过![]() 步(包含
步(包含![]() 步)的两名教师与大家分享心得,求被选取的两名教师恰好都在
步)的两名教师与大家分享心得,求被选取的两名教师恰好都在![]() 步(包含
步(包含![]() 步)以上的概率.
步)以上的概率.