ЬтФПФкШн
ЁОЬтФПЁПЯТУцЪЧаЁЖЋЩшМЦЕФЁАЙ§жБЯпЩЯвЛЕузїетЬѕжБЯпЕФДЙЯпЁБЕФГпЙцзїЭМЙ§ГЬЃЎ
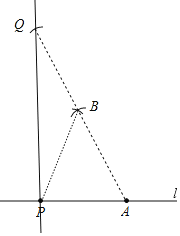
вбжЊЃКжБЯпlМАжБЯпlЩЯвЛЕуPЃЎ
![]()
ЧѓзїЃКжБЯпPQЃЌЪЙЕУPQЁЭlЃЎ
зїЗЈЃКШчЭМЃЌ
![]()
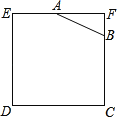
ЂйдкжБЯпlЩЯШЁвЛЕуAЃЈВЛгыЕуPжиКЯЃЉЃЌЗжБ№вдЕуPЃЌAЮЊдВаФЃЌAPГЄЮЊАыОЖЛЛЁЃЌСНЛЁдкжБЯпlЕФЩЯЗНЯрНЛгкЕуBЃЛ
ЂкзїЩфЯпABЃЌвдЕуBЮЊдВаФЃЌAPГЄЮЊАыОЖЛЛЁЃЌНЛABЕФбгГЄЯпгкЕуQЃЛ
ЂлзїжБЯпPQЃЎ
ЫљвджБЯпPQОЭЪЧЫљЧѓзїЕФжБЯпЃЎ
ИљОнаЁЖЋЩшМЦЕФГпЙцзїЭМЙ§ГЬЃЌ
ЃЈ1ЃЉЪЙгУжБГпКЭдВЙцЃЌВЙШЋЭМаЮЃЛЃЈБЃСєзїЭМКлМЃЃЉ
ЃЈ2ЃЉЭъГЩЯТУцЕФжЄУїЃЎ
жЄУїЃКСЌНгBPЃЌ
ЁпЁЁ ЁЁЃНЁЁ ЁЁЃНЁЁ ЁЁЃНAPЃЌ
ЁрЕуAЃЌPЃЌQдквдЕуBЮЊдВаФЃЌAPГЄЮЊАыОЖЕФдВЩЯЃЎ
ЁрЁЯAPQЃН90ЁуЃЈЁЁ ЁЁЃЉЃЎЃЈЬюаДЭЦРэЕФвРОнЃЉ
МДPQЁЭlЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉBPЃЌBAЃЌBQЃЌжБОЖЫљЖдЕФдВжмНЧЪЧжБНЧ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнаЁЖЋЩшМЦЕФГпЙцзїЭМЙ§ГЬЃЌгУжБГпКЭдВЙцзїЭММДПЩЃЛ
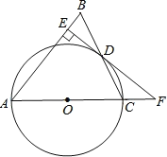
ЃЈ2ЃЉжЄУїЫМТЗЮЊЃКгЩзїЭМЙ§ГЬПЩжЊ![]() ЃЌДгЖјПЩЕУЕуAЃЌPЃЌQдквдЕуBЮЊдВаФЃЌAPГЄЮЊАыОЖЕФдВЩЯЃЌдйИљОндВжмНЧЖЈРэМДПЩжЄ.
ЃЌДгЖјПЩЕУЕуAЃЌPЃЌQдквдЕуBЮЊдВаФЃЌAPГЄЮЊАыОЖЕФдВЩЯЃЌдйИљОндВжмНЧЖЈРэМДПЩжЄ.
ЃЈ1ЃЉИљОнаЁЖЋЩшМЦЕФГпЙцзїЭМЙ§ГЬЃЌгУжБГпКЭдВЙцзїЭМНсЙћШчЯТЫљЪОЃК
ЃЈ2ЃЉжЄУїЃКСЌНгBP
![]()
ЁрЕуAЃЌPЃЌQдквдЕуBЮЊдВаФЃЌAPГЄЮЊАыОЖЕФдВЩЯ
![]() ЃЈжБОЖЫљЖдЕФдВжмНЧЪЧжБНЧЃЉ
ЃЈжБОЖЫљЖдЕФдВжмНЧЪЧжБНЧЃЉ
МД![]()
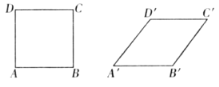
ЙЪД№АИЮЊBPЃЌBAЃЌBQЃЛжБОЖЫљЖдЕФдВжмНЧЪЧжБНЧ.

 ЧЇРяТэзпЯђМйЦкЦкФЉЗТецЪдОэКЎМйЯЕСаД№АИ
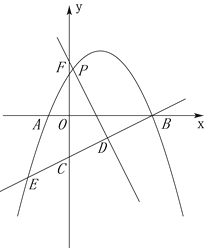
ЧЇРяТэзпЯђМйЦкЦкФЉЗТецЪдОэКЎМйЯЕСаД№АИЁОЬтФПЁПвбжЊХзЮяЯпyЃНax2+bx+c(aЁй0)ЩЯВПЗжЕуЕФКсзјБъxгызнзјБъyЕФЖдгІжЕШчЯТБэЃК
x | Ё | Љ3 | Љ2 | Љ1 | 0 | 1 | 2 | 3 | Ё |
y | Ё |
| Љ4 |
| Љ4 |
| 0 |
| Ё |
(1)ЧѓИУХзЮяЯпЕФБэДяЪНЃЛ
(2)вбжЊЕуE(4ЃЌ y)ЪЧИУХзЮяЯпЩЯЕФЕуЃЌЕуEЙигкХзЮяЯпЕФЖдГЦжсЖдГЦЕФЕуЮЊЕуFЃЌЧѓЕуEКЭЕуFЕФзјБъЃЎ