题目内容
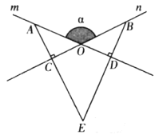
【题目】如图,已知半圆O的直径AB=4,沿它的一条弦折叠.若折叠后的圆弧与直径AB相切于点D,且AD:DB=3:1,则折痕EF的长______.
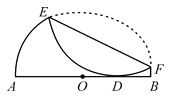
【答案】![]() .
.
【解析】
解:如图,过O作弦BC的垂线OP,垂足为D,分别与弧的交点为A、G,过切点F作PF⊥半径OC交OP于P点,
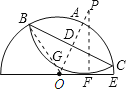
∵OP⊥BC,∴BD=DC,即OP为BC的中垂线. ∴OP必过弧BGC所在圆的圆心
又∵OE为弧BGC所在圆的切线,PF⊥OE,∴PF必过弧BGC所在圆的圆心
∴点P为弧BGC所在圆的圆心
∵弧BAC沿BC折叠得到弧BGC,∴⊙P为半径等于⊙O的半径,即PF=PG=OE=2,并且AD=GD
∴OG=AP
而F点分⊙O的直径为3:1两部分,∴OF=1
在Rt△OPF中,设OG=x,则OP=x+2,
∴OP2=OF2+PF2,即(x+2)2=12+22,解得x=![]()
∴AG=2-(![]() )=
)=![]()
∴DG=![]()
∴OD=OG+DG=![]()
在Rt△OBD中,BD2=OB2+OD2,即BD2=22-(![]() )2,
)2,
∴BD=![]()
∴BC=2BD=![]()
故答案为:![]() .
.

【题目】某水果公司新购进10000千克柑橘,每千克柑橘的成本为9元. 柑橘在运输、存储过程中会有损坏,销售人员从所有的柑橘中随机抽取若干柑橘,进行“柑橘损坏率”统计,并把获得的数据记录如下:
柑橘总重量n/千克 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
损坏柑橘重量m/千克 | 5.50 | 10.50 | 15.15 | 19.42 | 24.25 | 30.93 | 35.32 | 39.24 | 44.57 | 51.54 |
柑橘损坏的频率 | 0.110 | 0.105 | 0.101 | 0.097 | 0.097 | 0.103 | 0.101 | 0.098 | 0.099 | 0.103 |
根据以上数据,估计柑橘损坏的概率为 (结果保留小数点后一位);由此可知,去掉损坏的柑橘后,水果公司为了不亏本,完好柑橘每千克的售价至少为________元.