题目内容
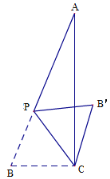
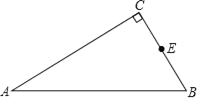
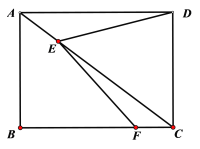
【题目】如图,矩形ABCD的对角线上有动点E,连结DE,边BC上有一定点F,连接EF,已知AB=3cm,AD=4cm,设A,E两点间的距离为![]() cm,D,E两点间的距离为
cm,D,E两点间的距离为![]() cm,E,F两点间的距离为
cm,E,F两点间的距离为![]() cm.
cm.
小胜根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量x的变化而变化的规律进行了探究.下面是小胜的探究过程,请补充完整:
随自变量x的变化而变化的规律进行了探究.下面是小胜的探究过程,请补充完整:
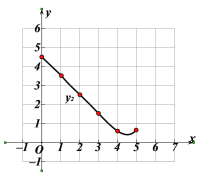
(1)按照下表中自变量x的值进行取点、画图、测量,得到x与y的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 |
| 4.00 | 3.26 | 2.68 | _______ | 2.53 | 3.00 |
| 4.50 | 3.51 | 2.51 | 1.53 | 0.62 | 0.65 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点![]() ,并画出函数
,并画出函数![]() 的图像:
的图像:
(3)结合函数图像,解决问题:当DE>EF时,AE的长度范围约为_________________cm.
【答案】(1)2.41;(2)作图见解析;(3)1.68<AE≤5.
【解析】
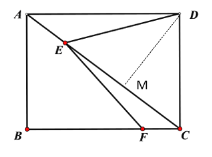
(1)过点D作DM⊥AC,然后利用勾股定理和直角三角形面积法求得![]() ,再取x=3结合勾股定理求出y1的值;
,再取x=3结合勾股定理求出y1的值;
(2)利用描点法画图即可;
(3)由图象可知,即可得出结论.
解:(1)过点D作DM⊥AC
由题意可知:在矩形ABCD中,AD=4,CD=AB=3
∴在Rt△ADC中,![]()
![]()
又∵DM⊥AC
∴在Rt△ADM中,![]()
所以当x=3时,即AE=3
此时EM=3.2-3=0.2
∴在Rt△DEM中,![]()
∴x=3时,![]()
故答案为:2.41;
(2)作图如下:
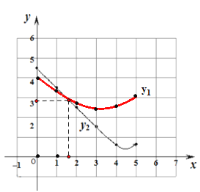
(3)如图;当![]() 时,
时,![]()
∴当DE>EF时,1.68<AE≤5
故答案为:1.68<AE≤5.

 阅读快车系列答案
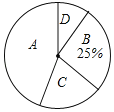
阅读快车系列答案【题目】某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程,为了解学生对这四门校本课程的喜爱情况,对学生进行了随机问卷调査(问卷调査表如图所示),将调査结果整理后绘制例图1、图2两幅均不完整的统计图表.
最受欢迎的校本课程调查问卷
您好!这是一份关于您最喜欢的校本课程问卷调查表,请在表格中选择一个(只能选一个)您最喜欢的课程选项,在其后空格内打“√”,非常感谢您的合作.
选项 | 校本课程 | |
A | 3D打印 | |
B | 数学史 | |
C | 诗歌欣赏 | |
D | 陶艺制作 |
校本课程 | 频数 | 频率 |
A | 36 | 0.45 |
B | 0.25 | |
C | 16 | b |
D | 8 | |
合计 | a | 1 |
请您根据图表中提供的信息回答下列问题:
(1)统计表中的a= ,b= ;
(2)“D”对应扇形的圆心角为 度;
(3)根据调査结果,请您估计该校2000名学生中最喜欢“数学史”校本课程的人数;
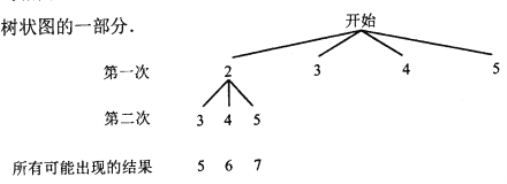
(4)小明和小亮参加校本课程学习,若每人从“A”、“B”、“C”三门校本课程中随机选取一门,请用画树状图或列表格的方法,求两人恰好选中同一门校本课程的概率.