ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌжБЯпl1ЃКyЃНkx+bгыЫЋЧњЯпyЃН![]() ЃЈxЃО0ЃЉНЛгкAЃЌBСНЕуЃЌгыxжсНЛгкЕуCЃЌгыyжсНЛгкЕуEЃЌвбжЊЕуAЃЈ1ЃЌ3ЃЉЃЌЕуCЃЈ4ЃЌ0ЃЉЃЎ
ЃЈxЃО0ЃЉНЛгкAЃЌBСНЕуЃЌгыxжсНЛгкЕуCЃЌгыyжсНЛгкЕуEЃЌвбжЊЕуAЃЈ1ЃЌ3ЃЉЃЌЕуCЃЈ4ЃЌ0ЃЉЃЎ
ЃЈ1ЃЉЧѓжБЯпl1КЭЫЋЧњЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉНЋЁїOCEбижБЯпl1ЗелЃЌЕуOТфдкЕквЛЯѓЯоФкЕФЕуHДІЃЌЧѓЕуHЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМЃЌЙ§ЕуEзїжБЯпl2ЃКyЃН3x+4НЛxжсЕФИКАыжсгкЕуFЃЌдкжБЯпl2ЩЯЪЧЗёДцдкЕуPЃЌЪЙЕУSЁїPBCЃНSЁїOBCЃПШєДцдкЃЌЧыжБНгаДГіЫљгаЗћКЯЬѕМўЕФЕуPЕФзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
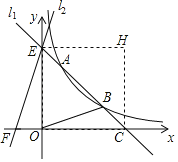
ЁОД№АИЁПЃЈ1ЃЉyЃНЉx+4ЃЌyЃН![]() ЃЈxЃО0ЃЉЃЛЃЈ2ЃЉHЃЈ4ЃЌ4ЃЉЃЛЃЈ3ЃЉДцдкЃЌЕуPЕФзјБъЮЊЃЈЉ1ЃЌ1ЃЉЛђЃЈ1ЃЌ7ЃЉЃЎ
ЃЈxЃО0ЃЉЃЛЃЈ2ЃЉHЃЈ4ЃЌ4ЃЉЃЛЃЈ3ЃЉДцдкЃЌЕуPЕФзјБъЮЊЃЈЉ1ЃЌ1ЃЉЛђЃЈ1ЃЌ7ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉНЋвбжЊЕузјБъДњШыКЏЪ§БэДяЪНЃЌМДПЩЧѓНтЃЛ
ЃЈ2ЃЉжЄУїOCЃНOEЃН4ЃЌгЩЗелЕУЁїCEHЁеЁїCEOЃЌНјЖјжЄУїЫФБпаЮOCHEЪЧе§ЗНаЮЃЌМДПЩЧѓНтЃЛ
ЃЈ3ЃЉЙ§ЕуOзїжБЯпmЁЮBCНЛжБЯпl2гкЕуPЁфЃЌдкxжсШЁЕуHЃЌЪЙOCЃНCHЃЈМДЕШМфИєЃЉЃЌЙ§ЕуHзїжБЯпnЁЮBCНЛжБЯпl2гкЕуPЃЌдђЕуPЃЈPЁфЃЉЮЊЫљЧѓЕуЃЌМДПЩЧѓНтЃЎ
НтЃКЃЈ1ЃЉНЋAЃЈ1ЃЌ3ЃЉЃЌCЃЈ4ЃЌ0ЃЉДњШыyЃНkx+bЃЌЕУ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
ЁржБЯпl1ЕФНтЮіЪНЮЊyЃНЉx+4ЃЎ
НЋAЃЈ1ЃЌ3ЃЉДњШыyЃН![]() ЃЈxЃО0ЃЉЃЌЕУmЃН3ЃЌ
ЃЈxЃО0ЃЉЃЌЕУmЃН3ЃЌ
ЁрЫЋЧњЯпЕФНтЮіЪНЮЊyЃН![]() ЃЈxЃО0ЃЉЃЛ
ЃЈxЃО0ЃЉЃЛ
ЃЈ2ЃЉНЋxЃН0ДњШыyЃНЉx+4ЃЌЕУyЃН4ЃЌ
ЁрEЃЈ0ЃЌ4ЃЉЃЎ
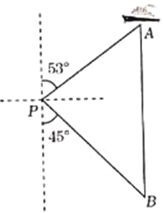
ЁрЁїCOEЪЧЕШбќжБНЧШ§НЧаЮЃЎ
ЁрЁЯOCEЃНЁЯOECЃН45ЁуЃЌOCЃНOEЃН4ЃЎ
гЩЗелЕУЁїCEHЁеЁїCEOЃЌ
ЁрЁЯCOEЃНЁЯCHEЃНЁЯOCHЃН90ЁуЃЎ
ЁрЫФБпаЮOCHEЪЧе§ЗНаЮЃЎ
ЁрHЃЈ4ЃЌ4ЃЉЃЛ
ЃЈ3ЃЉДцдкЃЌРэгЩЃК
ШчЭМЃЌЙ§ЕуOзїжБЯпmЁЮBCНЛжБЯпl2гкЕуP'ЃЌ
дкxжсШЁЕуHЃЌЪЙOCЃНCHЃЈМДЕШМфИєЃЉЃЌЙ§ЕуHзїжБЯпnЁЮBCНЛжБЯпl2гкЕуPЃЌ

SЁїPBCЃНSЁїOBCЃЌИљОнЭЌЕзЕШИпЕФСНИіШ§НЧаЮУцЛ§ЯрЕШЃЌдђЕуPЃЈP'ЃЉЮЊЫљЧѓЕуЃЎ
жБЯпBCБэДяЪНжаЕФkжЕЮЊЉ1ЃЌдђжБЯпmЁЂnБэДяЪНжаЕФkжЕвВЮЊЉ1ЃЌ
ЙЪжБЯпmЕФБэДяЪНЮЊЃКyЃНЉxЂйЃЌ
жБЯпl2ЕФБэДяЪНЮЊЃКyЃН3x+4ЂкЃЌ
СЊСЂЂйЂкВЂНтЕУЃКxЃНЉ1ЃЌyЃН1ЃЌЙЪЕуP'ЃЈЉ1ЃЌ1ЃЉЃЛ
ЩшжБЯпnЕФБэДяЪНЮЊЃКyЃНЉx+sЃЌЖјЕуHЃЈ8ЃЌ0ЃЉЃЌ
НЋЕуHЕФзјБъДњШыЩЯЪНВЂНтЕУЃКsЃН8ЃЌ
ЙЪжБЯпnЕФБэДяЪНЮЊЃКyЃНЉx+8ЂлЃЌ
СЊСЂЂкЂлВЂНтЕУЃКxЃН1ЃЌyЃН7ЃЌ
ЙЪЕуPЕФзјБъЮЊЃЈ1ЃЌ7ЃЉЃЛ
злЩЯЃЌЕуPЕФзјБъЮЊЃЈЉ1ЃЌ1ЃЉЛђЃЈ1ЃЌ7ЃЉЃЎ

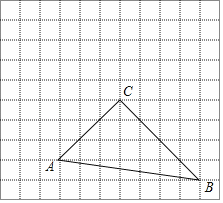
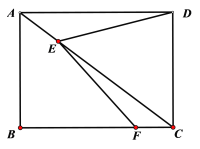
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDЕФЖдНЧЯпЩЯгаЖЏЕуEЃЌСЌНсDEЃЌБпBCЩЯгавЛЖЈЕуFЃЌСЌНгEFЃЌвбжЊAB=3cmЃЌAD=4cmЃЌЩшAЃЌEСНЕуМфЕФОрРыЮЊ![]() cmЃЌDЃЌEСНЕуМфЕФОрРыЮЊ
cmЃЌDЃЌEСНЕуМфЕФОрРыЮЊ![]() cmЃЌEЃЌFСНЕуМфЕФОрРыЮЊ
cmЃЌEЃЌFСНЕуМфЕФОрРыЮЊ![]() cmЃЎ
cmЃЎ
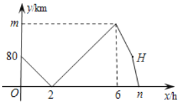
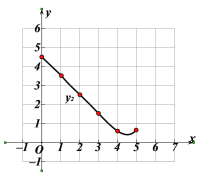
аЁЪЄИљОнбЇЯАКЏЪ§ЕФОбщЃЌЗжБ№ЖдКЏЪ§![]() ЃЌ
ЃЌ![]() ЫцздБфСПxЕФБфЛЏЖјБфЛЏЕФЙцТЩНјааСЫЬНОПЃЎЯТУцЪЧаЁЪЄЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃК
ЫцздБфСПxЕФБфЛЏЖјБфЛЏЕФЙцТЩНјааСЫЬНОПЃЎЯТУцЪЧаЁЪЄЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃК
ЃЈ1ЃЉАДееЯТБэжаздБфСПxЕФжЕНјааШЁЕуЁЂЛЭМЁЂВтСПЃЌЕУЕНxгыyЕФМИзщЖдгІжЕЃК
x/cm | 0 | 1 | 2 | 3 | 4 | 5 |
| 4.00 | 3.26 | 2.68 | _______ | 2.53 | 3.00 |
| 4.50 | 3.51 | 2.51 | 1.53 | 0.62 | 0.65 |
ЃЈ2ЃЉдкЭЌвЛЦНУцжБНЧзјБъЯЕxOyжаЃЌУшГіВЙШЋКѓЕФБэжаИїзщЪ§жЕЫљЖдгІЕФЕу![]() ЃЌВЂЛГіКЏЪ§
ЃЌВЂЛГіКЏЪ§![]() ЕФЭМЯёЃК
ЕФЭМЯёЃК
ЃЈ3ЃЉНсКЯКЏЪ§ЭМЯёЃЌНтОіЮЪЬтЃКЕБDE>EFЪБЃЌAEЕФГЄЖШЗЖЮЇдМЮЊ_________________cmЃЎ
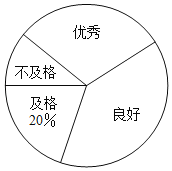
ЁОЬтФПЁПФГаЃЮЊСЫНтАЫФъМЖФаЩњЁАСЂЖЈЬјдЖЁБГЩМЈЕФЧщПіЃЌЫцЛњбЁШЁИУФъМЖВПЗжФаЩњНјааВтЪдЃЌвдЯТЪЧИљОнВтЪдГЩМЈЛцжЦЕФЭГМЦЭМБэЕФвЛВПЗжЃЎ
ГЩМЈЕШМЖ | ЦЕЪ§ЃЈШЫЃЉ | ЦЕТЪ |
гХау | 15 | 0.3 |
СМКУ | ||
МАИё | ||
ВЛМАИё | 5 |
ИљОнвдЩЯаХЯЂЃЌНтД№ЯТСаЮЪЬт
ЃЈ1ЃЉБЛВтЪдФаЩњжаЃЌГЩМЈЕШМЖЮЊЁАгХауЁБЕФФаЩњШЫЪ§ЮЊЁЁ ЁЁШЫЃЌГЩМЈЕШМЖЮЊЁАМАИёЁБЕФФаЩњШЫЪ§еМБЛВтЪдФаЩњзмШЫЪ§ЕФАйЗжБШЮЊЁЁ ЁЁ%ЃЛ
ЃЈ2ЃЉБЛВтЪдФаЩњЕФзмШЫЪ§ЮЊЁЁ ЁЁШЫЃЌГЩМЈЕШМЖЮЊЁАВЛМАИёЁБЕФФаЩњШЫЪ§еМБЛВтЪдФаЩњзмШЫЪ§ЕФАйЗжБШЮЊЁЁ ЁЁ%ЃЛ
ЃЈ3ЃЉШєИУаЃАЫФъМЖЙВга180УћФаЩњЃЌИљОнЕїВщНсЙћЃЌЙРМЦИУаЃАЫФъМЖФаЩњГЩМЈЕШМЖЮЊЁАСМКУЁБЕФбЇЩњШЫЪ§ЃЎ