题目内容
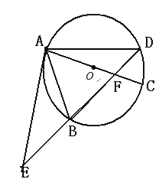
【题目】如图，在△ABC 中，∠ACB＝90°，AC＝12，BC＝5，P 是边 AB 上的动点（不与点 B 重合），将△BCP 沿 CP 所在的直线翻折，得到△B＇CP，连接 B＇A，B＇A 长度的最小值是 m，B＇A 长度的最大值是 n，则 m+n 的值等于 ______．
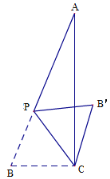
【答案】24
【解析】
先判断出B′A长度的最大值和B′A长度的最小值的位置，最后简单计算即可．
解：如图，
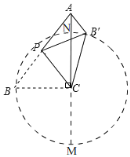
∵点P是直线AB上的动点，
∴△BCP沿CP所在的直线翻折得到△B'CP，点B落在以点C为圆心，BC为半径的圆上，延长AC交圆于M，
圆外一点到圆上的点的距离最大和最小的点是圆外一点过圆心的直线和圆的交点，
∴CM=CN=BC=6，
∴B′A长度的最小值是m=AN=AC-CN=12-5=7，
B′A长度的最大值是n=AM=AC+CM=12+5=17，
∴m+n=7+17=24；
故答案为24．
【题目】北京地铁票价计费标准如下表所示：
乘车距离 |
|
|
|
|
|
票价（元） | 3 | 4 | 5 | 6 | 每增加1元可乘坐20公里 |
另外，使用市政交通一卡通，每个自然月每张卡片支出累计满100元后，超出部分打8折；满150元后，超出部分打5折；支出累计达400元后，不再打折．小红妈妈上班时，需要乘坐地铁15公里到达公司，每天上下班共乘坐两次．如果每次乘坐地铁都使用市政交通一卡通，那么每月第21次乘坐地铁上下班时，她刷卡支出的费用（ ）
A.2.5元B.3元C.4元D.5元
【题目】某公司计划投资
万元引进一条汽车配件流水生产线，经过调研知道该流水生产线的年产量为
件，每件总成本为
万元，每件出厂价
万元；流水生产线投产后，从第
年到第
年的维修、保养费用累计
(万元)如下表：
第 |
|
|
|
|
|
| ··· |
维修、保养费用累计 |
|
|
|
|
|
| ··· |
若上表中第年的维修、保养费用累计(万元)与的数量关系符合我们已经学过的一次函数、二次函数、反比例函数中某一个．
（1）求出关于的函数解析式；
（2）投产第几年该公司可收回万元的投资？
（3）投产多少年后，该流水线要报废(规定当年的盈利不大于维修、保养费用累计即报费)？
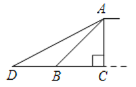
【题目】如图，矩形ABCD的对角线上有动点E，连结DE，边BC上有一定点F，连接EF，已知AB=3cm，AD=4cm，设A，E两点间的距离为
cm，D，E两点间的距离为
cm，E，F两点间的距离为
cm．
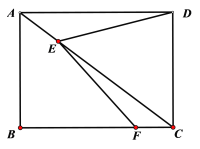
小胜根据学习函数的经验，分别对函数， 随自变量x的变化而变化的规律进行了探究．下面是小胜的探究过程，请补充完整：
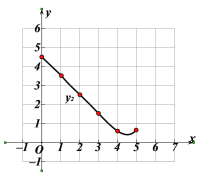
（1）按照下表中自变量x的值进行取点、画图、测量，得到x与y的几组对应值：
x/cm | 0 | 1 | 2 | 3 | 4 | 5 |
| 4.00 | 3.26 | 2.68 | _______ | 2.53 | 3.00 |
| 4.50 | 3.51 | 2.51 | 1.53 | 0.62 | 0.65 |
（2）在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点
，并画出函数
的图像：
（3）结合函数图像，解决问题：当DE>EF时，AE的长度范围约为_________________cm．
