题目内容
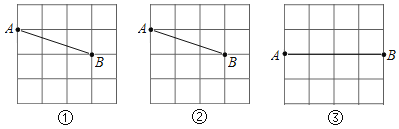
【题目】图①,图②,图③均为4×4的正方形网格,每个小正方形的顶点称为格点,小正方形的边长都为1.线段AB的端点均在格点上. 按要求在图①,图②,图③中画图.
(1)在图①中,以线段AB为斜边画一个等腰直角三角形,且直角的顶点为格点;
(2)在图②中,以线段AB为斜边画一个直角三角形,使其面积为2,且直角的顶点为格点;
(3)在图③中,画一个四边形,使所画四边形是中心对称图形,不是轴对称图形,且其余两个顶点均为格点.
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
(1)作AB的垂直平分线,垂直平分线在端点处的点即为顶点;
(2)如下图所示,满足面积条件和直角条件;
(3)以AB为对角线,绘制平行四边形即可
(1)如下图,过线段AB作垂直平分线,与网络交于格点C,则点C为等腰直角三角形顶点
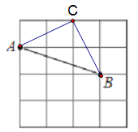
根据勾股定理,可求得AB=![]() ,AC=BC=
,AC=BC=![]()
根据勾股定理逆定理,可得△ABC是直角三角形,满足条件
(2)图形如下:
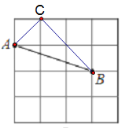
根据勾股定理,可求得:AB=![]() ,AC=
,AC=![]() ,BC=
,BC=![]()
根据勾股定理逆定理,可判断△ACB是直角三角形
面积=![]() ×
×![]() =2,成立
=2,成立
(3)平行四边形满足是中心对称图形,不是轴对称图形,图形如下:
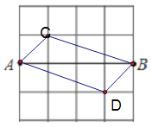
(答案不唯一)

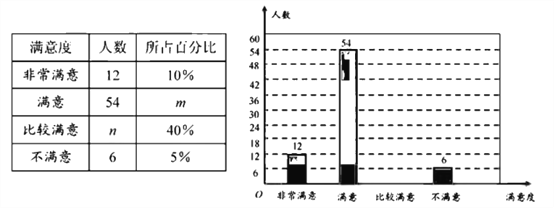
【题目】某校初三进行了第三次模拟考试,该校领导为了了解学生的数学考试情况,抽样调查部分学生的数学成绩,并将抽样的数据进行了如下整理:
①如下分数段整理样本;
等级等级 | 分数段 | 各组总分 | 人数 |
A | 110<X<120 | P | 4 |
B | 100<X<110 | 843 | n |
C | 90<X≤100 | 574 | m |
D | 80<X<90 | 171 | 2 |
②根据左表绘制扇形统计图.

(1)填空m= ,n= ,数学成绩的中位数所在的等级 ;
(2)如果该校有1200名学生参加了本次模拟测,估计D等级的人数;
(3)已知抽样调查学生的数学成绩平均分为102分,求A等级学生的数学成绩的平均分数.
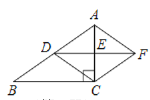
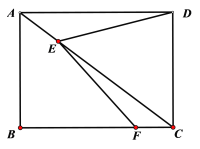
【题目】如图,矩形ABCD的对角线上有动点E,连结DE,边BC上有一定点F,连接EF,已知AB=3cm,AD=4cm,设A,E两点间的距离为![]() cm,D,E两点间的距离为
cm,D,E两点间的距离为![]() cm,E,F两点间的距离为
cm,E,F两点间的距离为![]() cm.
cm.
小胜根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量x的变化而变化的规律进行了探究.下面是小胜的探究过程,请补充完整:
随自变量x的变化而变化的规律进行了探究.下面是小胜的探究过程,请补充完整:
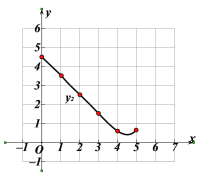
(1)按照下表中自变量x的值进行取点、画图、测量,得到x与y的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 |
| 4.00 | 3.26 | 2.68 | _______ | 2.53 | 3.00 |
| 4.50 | 3.51 | 2.51 | 1.53 | 0.62 | 0.65 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点![]() ,并画出函数
,并画出函数![]() 的图像:
的图像:
(3)结合函数图像,解决问题:当DE>EF时,AE的长度范围约为_________________cm.