题目内容
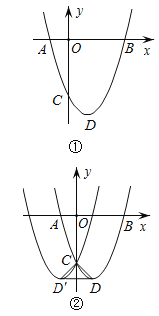
【题目】如图①,在平面直角坐标系中,抛物线![]() (
(![]() )与x轴相交于A,B两点,与y轴相交于点C,顶点为D.
)与x轴相交于A,B两点,与y轴相交于点C,顶点为D.
(1)当a=1时,抛物线顶点D的坐标为________,AB=_________;
(2)AB的长是否与a有关?说明你的理由;
(3)若将抛物线![]() (
(![]() )沿y轴折叠,得到另一抛物线,其顶点为D,如图②.连接CD,CD和DD.
)沿y轴折叠,得到另一抛物线,其顶点为D,如图②.连接CD,CD和DD.
①若△CDD为等边三角形时,则a=______;
②若△CDD为等腰直角三角形时,则a=______.
【答案】(1)(1,-4),4;(2)AB的长与a无关,见解析;(3)①![]() ; ② 1
; ② 1
【解析】
(1)将a=1代入解析式,并将解析式变形为顶点式,得到顶点坐标;另y=0得到点A、B的坐标;
(2)A、B是抛物线与x轴的交点,先求解出A、B两点的坐标,根据坐标求解距离,看计算得出的结果中是否含有字母a;
(3)①求解出点C、D、D的坐标(用a表示),利用等边三角形三边相等的性质求解a;
②同上,先得出坐标点,利用勾股股定理的逆定理列写等式求解a
(1)将a=1代入解析式得:![]()
变形为顶点式为:![]()
∴顶点坐标为:(1,-4)
另y=0得:![]()
解得:x=-1或x=3
设点A在点B的左侧
∴A(-1,0),B(3,0)
∴AB=4
(2)AB的长与a无关
理由是:当y=0时,
![]() .
.
解得![]() ,
,![]() .
.
∴A(-1,0),B(3,0).
∴AB=3-(-1)= 4.
∴AB的长与a无关
(3)①抛物线![]()
点C为与y轴的交点,即x=0
得:y=-3a,∴C(0,-3a)
将抛物线变形为顶点式为:![]()
故顶点D(1,-4a)
∵D与点D关于y轴对称
∴D(-1,4a)
∴DD=2,CD=![]()
∵△CDD是等边三角形
∴DD=CD,即2=![]()
解得:a=![]()
②∵CD=CD,∴△CDD肯定是等腰三角形
∵△CDD是等腰直角三角形
∴![]() ,即:
,即:![]()
解得:a=1

【题目】北京地铁票价计费标准如下表所示:
乘车距离 |
|
|
|
|
|
票价(元) | 3 | 4 | 5 | 6 | 每增加1元可乘坐20公里 |
另外,使用市政交通一卡通,每个自然月每张卡片支出累计满100元后,超出部分打8折;满150元后,超出部分打5折;支出累计达400元后,不再打折.小红妈妈上班时,需要乘坐地铁15公里到达公司,每天上下班共乘坐两次.如果每次乘坐地铁都使用市政交通一卡通,那么每月第21次乘坐地铁上下班时,她刷卡支出的费用( )
A.2.5元B.3元C.4元D.5元
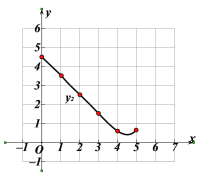
【题目】如图,矩形ABCD的对角线上有动点E,连结DE,边BC上有一定点F,连接EF,已知AB=3cm,AD=4cm,设A,E两点间的距离为![]() cm,D,E两点间的距离为
cm,D,E两点间的距离为![]() cm,E,F两点间的距离为
cm,E,F两点间的距离为![]() cm.
cm.
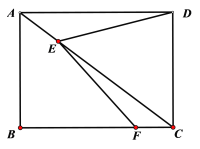
小胜根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量x的变化而变化的规律进行了探究.下面是小胜的探究过程,请补充完整:
随自变量x的变化而变化的规律进行了探究.下面是小胜的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,得到x与y的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 |
| 4.00 | 3.26 | 2.68 | _______ | 2.53 | 3.00 |
| 4.50 | 3.51 | 2.51 | 1.53 | 0.62 | 0.65 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点![]() ,并画出函数
,并画出函数![]() 的图像:
的图像:
(3)结合函数图像,解决问题:当DE>EF时,AE的长度范围约为_________________cm.