题目内容
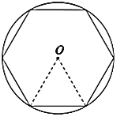
【题目】中国魏晋时期的数学家刘徽首创“割圆术”,奠定了中国圆周率计算在世界上的领先地位.刘徽提出:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”,由此求得圆周率![]() 的近似值.如图,设半径为
的近似值.如图,设半径为![]() 的圆内接正
的圆内接正![]() 边形的周长为
边形的周长为![]() ,圆的直径为
,圆的直径为![]() ,当
,当![]() 时,
时,![]() ,则当
,则当![]() 时,
时,![]() ______.(结果精确到0.01,参考数据:
______.(结果精确到0.01,参考数据:![]() ,
,![]()
![]() )
)
【答案】3.11
【解析】
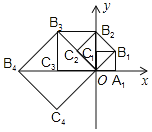
圆的内接正十二边形被半径分成顶角为30°的十二个等腰三角形,作辅助线构造直角三角形,根据中心角的度数以及半径的大小,求得C=24r·sin15°,d=2r,进而得到答案.
解:如图,圆的内接正十二边形被半径分成12个如图所示的等腰三角形,其顶角为30°,即∠AOB=30°,
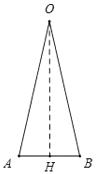
作OH⊥AB于点H,则∠AOH=15°,
∵AO=BO=r,
在Rt△AOH中,sin∠AOH=![]() ,即sin15°=
,即sin15°=![]() ,
,
∴AH=r·sin15°,AB=2AH=2r·sin15°,
∴C=12·2r·sin15°=24r·sin15°,
又∵d=2r,
∴![]() ,
,
故答案为:3.11.

 阅读快车系列答案
阅读快车系列答案【题目】某校初三进行了第三次模拟考试,该校领导为了了解学生的数学考试情况,抽样调查部分学生的数学成绩,并将抽样的数据进行了如下整理:
①如下分数段整理样本;
等级等级 | 分数段 | 各组总分 | 人数 |
A | 110<X<120 | P | 4 |
B | 100<X<110 | 843 | n |
C | 90<X≤100 | 574 | m |
D | 80<X<90 | 171 | 2 |
②根据左表绘制扇形统计图.

(1)填空m= ,n= ,数学成绩的中位数所在的等级 ;
(2)如果该校有1200名学生参加了本次模拟测,估计D等级的人数;
(3)已知抽样调查学生的数学成绩平均分为102分,求A等级学生的数学成绩的平均分数.
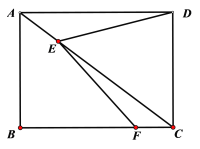
【题目】如图,矩形ABCD的对角线上有动点E,连结DE,边BC上有一定点F,连接EF,已知AB=3cm,AD=4cm,设A,E两点间的距离为![]() cm,D,E两点间的距离为
cm,D,E两点间的距离为![]() cm,E,F两点间的距离为
cm,E,F两点间的距离为![]() cm.
cm.
小胜根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量x的变化而变化的规律进行了探究.下面是小胜的探究过程,请补充完整:
随自变量x的变化而变化的规律进行了探究.下面是小胜的探究过程,请补充完整:
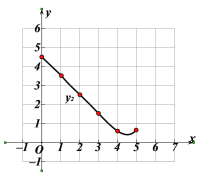
(1)按照下表中自变量x的值进行取点、画图、测量,得到x与y的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 |
| 4.00 | 3.26 | 2.68 | _______ | 2.53 | 3.00 |
| 4.50 | 3.51 | 2.51 | 1.53 | 0.62 | 0.65 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点![]() ,并画出函数
,并画出函数![]() 的图像:
的图像:
(3)结合函数图像,解决问题:当DE>EF时,AE的长度范围约为_________________cm.