题目内容
【题目】如图,已知在△ABC中,∠ACB=90°,BC=2,AC=4,点D在射线BC上,以点D为圆心,BD为半径画弧交边AB于点E,过点E作EF⊥AB交边AC于点F,射线ED交射线AC于点G.
(1)求证:△EFG∽△AEG;
(2)设FG=x,△EFG的面积为y,求y关于x的函数解析式并写出定义域;
(3)联结DF,当△EFD是等腰三角形时,请直接写出FG的长度.



【答案】(1)详见解析;(2)![]() ;(3)当△EFD为等腰三角形时,FG的长度是:
;(3)当△EFD为等腰三角形时,FG的长度是: ![]() .
.
【解析】试题分析:(1)由等边对等角得∠B=∠BED,由同角的余角相等可得∠A=∠GEF,进而由两角分别相等的两个三角形相似,可证△EFG∽△AEG;
(2)作EH⊥AF于点H,由tanA=![]() 及△EFG∽△AEG,得AG=4x,AF=3x,EH=
及△EFG∽△AEG,得AG=4x,AF=3x,EH= ![]() ,
,
可得y关于x的解析式;
(3)△EFD是等腰三角形,分三种情况讨论:①EF=ED;②ED=FD;③ED=EF三种情况讨论即可.
试题解析:(1)∵ ED=BD,
∴ ∠B=∠BED.
∵ ∠ACB=90°,
∴ ∠B+∠A=90°.
∵ EF⊥AB,
∴ ∠BEF=90°.
∴ ∠BED+∠GEF=90°.
∴ ∠A=∠GEF.
∵ ∠G是公共角,
∴ △EFG∽△AEG;
(2)作EH⊥AF于点H.
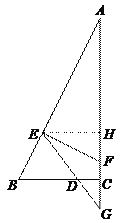
∵ 在Rt△ABC中,∠ACB=90°,BC=2,AC=4,
∴tanA=![]() =
=![]() ,
,
∴ 在Rt△AEF中,∠AEF=90°,tanA=![]() =
=![]() ,
,
∵ △EFG∽△AEG,
∴![]() ,
,
∵ FG=x,
∴ EG=2x,AG=4x.
∴ AF=3x.
∵ EH⊥AF,
∴ ∠AHE=∠EHF=90°.
∴ ∠EFA+∠FEH=90°.
∵ ∠AEF=90°,
∴ ∠A+∠EFA=90°,
∴ ∠A=∠FEH,
∴ tanA =tan∠FEH,
∴ 在Rt△EHF中,∠EHF=90°,tan∠FEH=![]() =
=![]() ,
,
∴ EH=2HF,
∵ 在Rt△AEH中,∠AHE=90°,tanA=![]() =
=![]() ,
,
∴ AH=2EH,
∴ AH=4HF,
∴ AF=5HF,
∴ HF= ![]() ,
,
∴EH= ![]() ,
,
∴y=![]() FG·EH=
FG·EH=![]() x·
x·![]() =
=![]() 定义域:(0<x≤
定义域:(0<x≤![]() );
);
(3)当△EFD为等腰三角形时,

①当ED=EF时,则有∠EDF=∠EFD,
∵∠BED=∠EFH,
∴∠BEH=∠AHG,
∵∠ACB=∠AEH=90°,
∴∠CEF=∠HEF,即EF为∠GEH的平分线,
则ED=EF=x,DG=8x,
∵anA=![]() ,
,
∴x=3,即BE=3;
②若FE=FD, 此时FG的长度是![]() ;
;
③若DE=DF, 此时FG的长度是![]() .
.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案