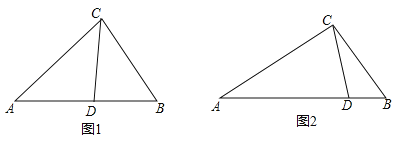题目内容
【题目】（1）（问题解决）已知点
在
内，过点分别作关于
、
的对称点
、
.
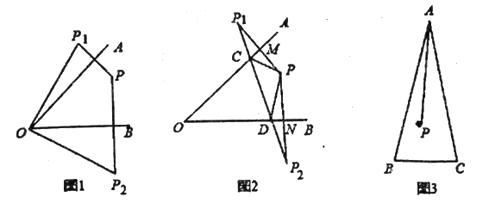
①如图1，若
，请直接写出
______；
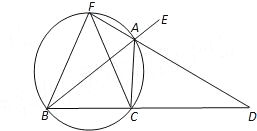
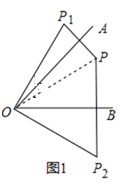
②如图2，连接
分别交、于
、
，若
，求的度数；
③在②的条件下，若
度（
），请直接写出
______度（用含
的代数式表示）.
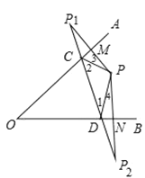
（2）（拓展延伸）利用“有一个角是
的等腰三角形是等边三角形”这个结论，解答问题：如图3，在
中，
，点是内部一定点，
，点
、
分别在边
、
上，请你在图3中画出使
周长最小的点、的位置（不写画法），并直接写出周长的最小值.
【答案】（1）【问题解决】①
；②
；③
；（2）【拓展延伸】如图，见解析；
周长最小值为8．
【解析】
（1）①连接OP，由点P关于直线OA的对称点
，点P关于直线OB的对称点
，可得
，
，再由
+
=2（
+
）=2
,即可求得∠AOB的度数；②由
，根据三角形的内角和定理可得
；由轴对称的性质得，
，
，再由三角形外角的性质可得
，
，所以
，即可求得
；由轴对称的性质可得
，由四边形的内角和为360°即可求得； ③类比②的方法即可解答；（2）作点P关于边AB的对称点，再作点P关于边AC的对称点 ，连结，分别交AB、AC于点E、F，此时的周长最小，最小为的长，由①的方法求得∠A=60°，A=A，再由“有一个角是
的等腰三角形是等边三角形”即可判定△A是等边三角形，根据等边三角形的性质可得=AP=8，由此即可得周长最小值为8．
（1）①连接OP，
∵点P关于直线OA的对称点，点P关于直线OB的对称点，
∴，，
∴+=2（+）=2
,
故答案为：50°；
②如图2，
∵，
∴，
由轴对称的性质得，，，
∵，，
∴，
∴
，
由轴对称的性质得，，
∴
；
③.
如图2，
∵
，
∴
，
由轴对称的性质得，，，
∵，，
∴
，
∴
，
由轴对称的性质得，，
∴
=
；
故答案为：；
（2）如图所示，的周长最小，周长最小值为8．
①画点P关于边AB的对称点，
②画点P关于边AC的对称点 ，
③连结，分别交AB、AC于点E、F，
此时的周长最小，周长最小值为8．
