题目内容
【题目】已知二次函数y＝ax2﹣2ax+k（a、k为常数，a≠0），线段AB的两个端点坐标分别为A(﹣1，2)，B(2，2)．
（1）该二次函数的图象的对称轴是直线 ；
（2）当a＝﹣1时，若点B(2，2)恰好在此函数图象上，求此二次函数的关系式；
（3）当a＝﹣1时，当此二次函数的图象与线段AB只有一个公共点时，求k的取值范围；
（4）若k＝a+3，过点A作x轴的垂线交x轴于点P，过点B作x轴的垂线交x轴于点Q，当﹣1＜x＜2，此二次函数图象与四边形APQB的边交点个数是大于0的偶数时，直接写出k的取值范围．
【答案】（1）x＝1；（2）y＝﹣x2+2x+2；（3）2＜k≤5或k＝1；（4）2≤k＜
或k＜0
【解析】
（1）根据二次函数y＝ax2﹣2ax+k（a、k为常数，a≠0）即可求此二次函数的对称轴；
（2）当a＝﹣1时，把B（2，2）代入即可求此二次函数的关系式；
（3）当a＝﹣1时，根据二次函数的图象与线段AB只有一个公共点，分三种情况说明：当抛物线顶点落在AB上时，k+1＝2，k＝1；当抛物线经过点B时，k＝2；当抛物线经过点A时，k＝5，即可求此k的取值范围；
（4）当k＝a+3，根据题意画出图形，观察图形即可求此k的取值范围．
解：（1）二次函数y＝ax2﹣2ax+k（a、k为常数，a≠0），
二次函数的图象的对称轴是直线x＝1．
故答案为x＝1；
（2）当a＝﹣1时，y＝﹣x2+2x+k
把B（2，2）代入，得 k＝2，
∴y＝﹣x2+2x+2
（3）当a＝﹣1时，
y＝﹣x2+2x+k
＝﹣（x﹣1）2+k+1
∵此二次函数的图象与线段AB只有一个公共点，
当抛物线顶点落在AB上时，k+1＝2，k＝1
当抛物线经过点B时，k＝2
当抛物线经过点A时，
﹣1﹣2+k＝2，k＝5
综上所述：2＜k≤5或k＝1；
（4）当k＝a+3时，
y＝ax2﹣2ax+a+3
＝a（x﹣1）2+3
所以顶点坐标为（1，3）
∴a+3＜3
∴a＜0．
如图，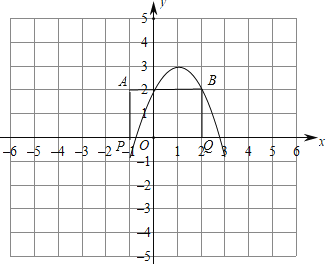
过点A作x轴的垂线交x轴于点P，过点B作x轴的垂线交x轴于点Q，
∴P（﹣1，0），Q（2，0）
当﹣1＜x＜2，此二次函数图象与四边形APQB的边交点个数是大于0的偶数，
当抛物线过点P时，
a+2a+a+3＝0，解得a＝﹣
∴k＝a+3＝，
当抛物线经过点B时，
4a﹣4a+a+3＝2，解得a＝﹣1，
∴k＝2，
当抛物线经过点Q时，
4a﹣4a+a+3＝0，解得a＝﹣3，
∴k＝0
综上所述：2≤k＜或k＜0．
