Question

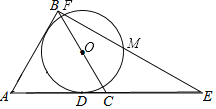
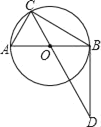
【题目】如图，AB是⊙O的直径，C为⊙O上一点，点D在CO的延长线上，连接BD．已知BC＝BD，AB＝4．

（1）若BC＝2，求证：BD是⊙O的切线；

（2）BC＝3，求CD的长．

Answer 1

【答案】（1）详见解析；（2）CD＝．

【解析】

（1）先证∠ACB＝90°，再求出sinA的值，求得∠A＝60°，得到△AOC为等边三角形，再求得∠BCD＝30°，利用三角形内角和定理即可得出结论；

（2）先求出半径，再证∠BCD＝∠D，∠D＝∠OBC，即可证得△BCD∽△OCB，列比例式把数值带入即可求出CD的长．

解：（1）∵AB为圆O的直径，

∴∠ACB＝90°，

在Rt△ABC中，∵sinA＝＝，

∴∠A＝60°，

∵AO＝CO，

∴△AOC为等边三角形，

∴∠AOC＝∠ACO＝60°，

∴∠BCD＝∠ACB﹣∠ACO＝90°﹣60°＝30°，

∵∠BOD＝∠AOC＝60°，

∴∠OBD＝180°﹣（∠BOD+∠D）＝90°，

∴OB⊥BD，

则BD为圆O的切线；

（2）∵AB为圆O的直径，且AB＝4，

∴OB＝OC＝2，

∵BC＝BD，

∴∠BCD＝∠D，

∵OC＝OB，

∴∠BCD＝∠OBC，

∴∠D＝∠OBC，

在△BCD和△OCB中，

∠D＝∠OBC，∠BCD＝∠OCB，

∴△BCD∽△OCB，

∴，即，

则CD＝．