Question

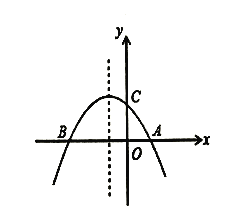
【题目】 如图，已知抛物线与轴交于两点，与轴交于点.

求点的坐标;

点是此抛物线上的点，点是其对称轴上的点，求以为顶点的平行四边形的面积;

Answer 1

【答案】（1）点坐标，点坐标，点坐标；（2）或.

【解析】

（1）令x=0,可求抛物线与y轴交点的坐标，令y=0，可求抛物线与x轴交点的坐标；

（2）当为平行四边形的对角线时，由对角线互相平分得此时E为抛物线的顶点；当AB为平行四边形的边时，由EF=AB=6求E点坐标，再根据平行四边形的面积公式求解.

解：（1）令得，

，或，

点坐标，点坐标，

令，得点坐标．

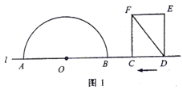
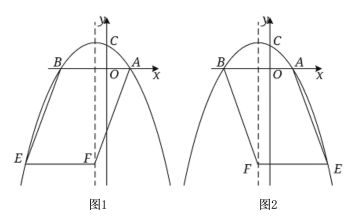
（2）如图1，图2，当为平行四边形的边时，

，对称轴，

点的横坐标为或，

点坐标或，此时点，

以为顶点的平行四边形的面积．

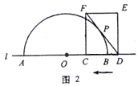
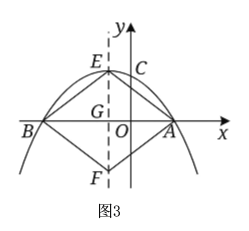
②如图3，当AB为对角线时时，此时E为抛物线的顶点

点，设对称轴与轴交点为，

令与相等，则四边形是菱形，

此时以为顶点的平行四边形的面积.

综上所述，以为顶点的平行四边形的面积或.