Question

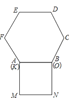
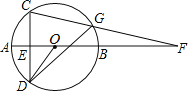
【题目】如图，AB是⊙O的直径，弦CD⊥AB于点E，点G为弧BC上一动点，CG与AB的延长线交于点F，连接OD．

（1）判定∠AOD与∠CGD的大小关系为　 　，并求证：GB平分∠DGF．

（2）在G点运动过程中，当GD＝GF时，DE＝4，BF＝，求⊙O的半径．

Answer 1

【答案】（1），证明见解析；（2）5.

【解析】

（1）由垂径定理得出，由圆周角定理即可得出∠AOD=∠CGD；连接BG、BC、BD，由垂径定理得出，由圆周角定理得出∠BCD=∠BGD=∠BDC，由四边形BDCG为圆内接四边形，得出∠BGF=∠BDC，推出∠BGD=∠BGF，即可得出结论；
（2）由SAS证得△BGD≌△BGF，得出BD=BF=4，由勾股定理得出BE=8，设⊙O的半径为r，则OE=8-r，在Rt△ODE中，根据勾股定理即可求得答案．

（1）∠AOD=∠CGD；理由如下：

∵AB是⊙O的直径，弦CD⊥AB，

∴，

∴∠AOD=∠CGD，

故答案为：∠AOD=∠CGD；

连接BG、BC、BD，如图所示：

∵AB是⊙O的直径，弦CD⊥AB，

∴，

∴∠BCD=∠BGD=∠BDC，

∵四边形BDCG为圆内接四边形，

∴∠BGF=∠BDC，

∴∠BGD=∠BGF，

∴GB平分∠DGF；

（2）在△BGD和△BGF中，，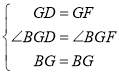

∴△BGD≌△BGF（SAS)，

∴BD=BF=4，

，

设⊙O的半径为r，则OE=8﹣r，

在Rt△ODE中，，

解得：，即⊙O的半径为5．