题目内容
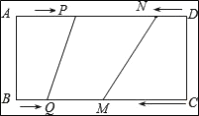
【题目】如图，在矩形ABCD中，BC=24cm，P，Q，M，N分别从A，B，C，D出发沿AD，BC，CB，DA方向在矩形的边上同时运动，当有一个点先到达所在运动边的另一个端点时，运动即停止．
已知在相同时间内，若BQ=x cm（x≠0），则AP=2x cm，CM=3x cm，DN=x2cm．
（1）当x为何值时，以P、N两点重合？
（2）问Q、M两点能重合吗？若Q、M两点能重合，则求出相应的x的值；若Q、M两点不能重合，请说明理由．
（3）当x为何值时，以P，Q，M，N为顶点的四边形是平行四边形．
【答案】（1）4；（2）点Q与点M不能重合．理由见解析；（3）x=2或x=﹣3+
.
【解析】解：（1）当点P与点N重合时，
由
，得
（舍去）
所以
时点P与点N重合 2分
（2） 当点Q与点M重合时，
由
，得
----------3分
此时
，不符合题意．
故点Q与点M不能重合．---------4分
（3）由（1）知，点Q 只能在点M的左侧，
① 当点P在点N的左侧时，
由
，
解得
．
当x=2时四边形PQMN是平行四边形． 6分
② 当点P在点N的右侧时，
由
，
解得
（舍去）．
当x=-3+
时四边形NQMP是平行四边形． 8分
综上：当x=2或x=-3+
时，以P，Q，M，N为顶点的四边形是平行四边形．
【题目】某市公共交通收费如下：
公交票价 | ||
里程（千米） | 票价（元） | 刷卡优惠后付款（元） |
0-10 | 2 | 1 |
10-15 | 3 | 1.5 |
15-20 | 4 | 2 |
20-25 | 5 | 2.5 |
25-30 | 6 | 3 |
以后每增加5千米 | 增加1元 | 增加0.5元 |
地铁票价 | |
里程（千米） | 票价（元） |
0-6 | 3 |
6-12 | 4 |
12-22 | 5 |
22-32 | 6 |
32-52 | 7 |
52-72 | 8 |
以后每增加20千米 | 增加1元 |
（公交票价10千米（含）内2元，不足10千米按10千米计算，其他里程类同；地铁票价6千米（含）内3元，不足6千米按6千米计算，其他里程类同）
（1）张阿姨周日去看望父母，可是张阿姨忘了带一卡通，请你帮助张阿姨思考两个问题：
①若到父母家无论乘公交车还是地铁距离都是24千米，选择哪种公交交通工具费用较少？
②若只用10元钱乘坐公交或地铁，选择哪种公共交通工具乘坐的里程更远？
（2）张阿姨下周日计划使用一卡通刷卡乘公共交通到景点游玩，若里程大于35千米且小于120千米，公交、地铁均可直达.请问：选择公交还是选择地铁出行更省钱？为什么？
