题目内容
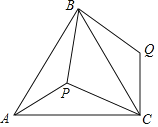
【题目】如图,在平行四边形ABCD中,点E是CD边上一点,![]() ,连接AE、BE、BD,且AE、BD交于点F.若
,连接AE、BE、BD,且AE、BD交于点F.若![]() ,则
,则![]() ( )
( )

A.15.5B.16.5C.17.5D.18.5
【答案】C
【解析】
根据已知可得到相似三角形,从而可得到其相似比,根据相似三角形的面积比等于相似比的平方求出△ABF,再根据同高的三角形的面积之比等于底的比得出△BEF的面积,则![]() =
= ![]() +
+![]() 即可求解.
即可求解.
解:∵四边形ABCD是平行四边形,
∴DE∥AB,
∴△DFE∽△BFA,
∵DE:EC=2:3,
∴DE:AB=2:5,DF:FB=2:5,
∵![]() =2,根据相似三角形的面积比等于相似比的平方,
=2,根据相似三角形的面积比等于相似比的平方,
∴![]() :
:![]() =
=![]() ,即
,即![]() =
=![]()
![]() =12.5,
=12.5,
∵同高的三角形的面积之比等于底的比,△DEF和△BEF分别以DF、FB为底时高相同,
∴![]() :
:![]() = DF:FB=2:5,即
= DF:FB=2:5,即![]() =
=![]()
![]() =5,
=5,
∴![]() =
= ![]() +
+![]() =12.5+5=17.5,
=12.5+5=17.5,
故选:C.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
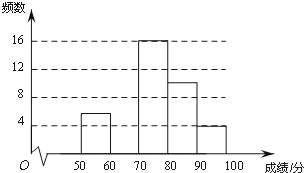
金博士一点全通系列答案【题目】为弘扬中华传统文化,了解学生整体听写能力,某校组织全校1000名学生进行一次汉字听写大赛初赛,从中抽取部分学生的成绩进行统计分析,根据测试成绩绘制出了频数分布表和频数分布直方图:
分组/分 | 频数 | 频率 |
50≤x<60 | 6 | 0.12 |
60≤x<70 | a | 0.28 |
70≤x<80 | 16 | 0.32 |
80≤x<90 | 10 | 0.20 |
90≤x≤100 | c | b |
合计 | 50 | 1.00 |
(1)表中的a=______,b=______,c=______;
(2)把上面的频数分布直方图补充完整,并画出频数分布折线图;
(3)如果成绩达到90及90分以上者为优秀,可推荐参加进入决赛,那么请你估计该校进入决赛的学生大约有多少人.
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?