题目内容
【题目】综合与探究
问题情境:
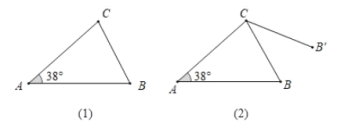
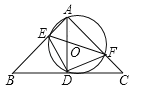
(1)如图1,两块等腰直角三角板△ABC和△ECD如图所示摆放,其中∠ACB=∠DCE=90°,点F,H,G分别是线段DE,AE,BD的中点,A,C,D和B,C,E分别共线,则FH和FG的数量关系是 ,位置关系是 .
合作探究:
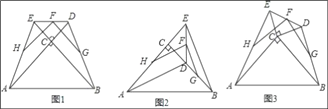
(2)如图2,若将图1中的△DEC绕着点C顺时针旋转至A,C,E在一条直线上,其余条件不变,那么(1)中的结论还成立吗?若成立,请证明,若不成立,请说明理由.
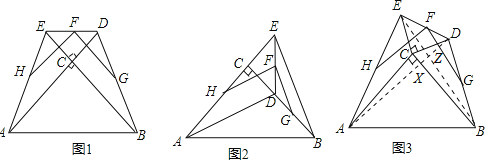
(3)如图3,若将图1中的△DEC绕着点C顺时针旋转一个锐角,那么(1)中的结论是否还成立?若成立,请证明,若不成立,请说明理由.
【答案】(1)FG=FH,FG⊥FH;(2)(1)中结论成立,证明见解析;
(3)(1)中的结论成立,结论是FH=FG,FH⊥FG.理由见解析.
【解析】试题分析:(1)证BE=AD,根据三角形的中位线推出FH=![]() AD,FH∥AD,FG=
AD,FH∥AD,FG=![]() BE,FG∥BE, 即可推出答案;
BE,FG∥BE, 即可推出答案;
(2)证△ACD≌△BCE,推出AD=BE,根据三角形的中位线定理即可推出答案;
(3)连接AD,BE,根据全等推出AD=BE,根据三角形的中位线定理即可推出答案.
试题解析:(1)∵CE=CD,AC=BC, ![]()
∴BE=AD,
∵F是DE的中点,H是AE的中点,G是BD的中点,
∴FH=![]() AD,FH∥AD,FG=
AD,FH∥AD,FG=![]() BE,FG∥BE,
BE,FG∥BE,
∴FH=FG,
∵AD⊥BE,
∴FH⊥FG,
故答案为:相等,垂直。
(2)答:成立,
证明:∵CE=CD, ![]() AC=BC,
AC=BC,
∴△ACD≌△BCE,
∴AD=BE,
由(1)知:FH=![]() AD,FH∥AD,FG=
AD,FH∥AD,FG=![]() BE,FG∥BE,
BE,FG∥BE,
∴FH=FG,FH⊥FG,
∴(1)中的猜想还成立.
(3)答:成立,结论是FH=FG,FH⊥FG.
连接AD,BE,两线交于Z,AD交BC于X,
同(1)可证
∴FH=![]() AD,FH∥AD,FG=
AD,FH∥AD,FG=![]() BE,FG∥BE,
BE,FG∥BE,
∵三角形ECD、ACB是等腰直角三角形,
∴CE=CD,AC=BC, ![]()
∴∠ACD=∠BCE,
在△ACD和△BCE中
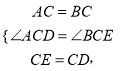
∴△ACD≌△BCE,
∴AD=BE,∠EBC=∠DAC,
∵![]() ∠CXA=∠DXB,
∠CXA=∠DXB,
∴![]()
∴![]() 即AD⊥BE,
即AD⊥BE,
∵FH∥AD,FG∥BE,
∴FH⊥FG,
即FH=FG,FH⊥FG,
结论是FH=FG,FH⊥FG

【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?