题目内容
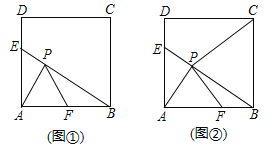
【题目】(1)知识延伸:如图1,在![]() 中,
中,![]() ,
,![]() ,根据三角函数的定义得:
,根据三角函数的定义得:![]() ;
;
(2)拓展运用:如图2,在锐角三角形![]() 中,
中,![]() .
.
①求证:![]() ;
;
②已知:![]() ,求
,求![]() 的度数.
的度数.

【答案】(1)1;(2) ①见解析;②60°.
【解析】分析:(1)利用三角函数定义直接计算即可;
(2)①过A作AD⊥BC于点D,设BD=x,则CD=a﹣x,利用勾股定理可分别表示出AD,整理则可证得结论;
②直接代入①中所得结论,可求得cosB的值,则可求得∠B的度数.
详解:(1)∵在△ABC中,∠C=90°,AB=c,BC=a,AC=b,∴sinA=![]() ,cosA=
,cosA=![]() ,且a2+b2=c2,∴sin2A+cos2A=(
,且a2+b2=c2,∴sin2A+cos2A=(![]() )2+(
)2+(![]() )2=
)2=![]() =
=![]() =1.
=1.
故答案为:1;
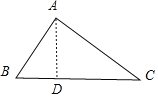
(2)①过A作AD⊥BC于点D,如图,设BD=x,则CD=a﹣x.在Rt△ABD中,由勾股定理可得AD2=AB2﹣BD2.在Rt△ACD中,由勾股定理可得AD2=AC2﹣CD2,∴AB2﹣BD2=AC2﹣CD2,即c2﹣x2=b2﹣(a﹣x)2,∴b2=a2+c2﹣2ax.在Rt△ABD中,cosB=![]() ,∴x=ccosB,∴b2=a2+c2﹣2accosB;
,∴x=ccosB,∴b2=a2+c2﹣2accosB;
②当a=3,b=![]() ,c=2时,代入①中结论,可得(
,c=2时,代入①中结论,可得(![]() )2=32+22﹣2×3×2cosB,∴cosB=
)2=32+22﹣2×3×2cosB,∴cosB=![]() ,∴∠B=60°.
,∴∠B=60°.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目