��Ŀ����
����Ŀ���Ķ��������ݣ�����Ҫ�������⣺ ���⣺����ƽ���ڣ���֪�ֱ���![]() ���㣬
���㣬![]() ���㣬
���㣬![]() ���㣬5 ���㣬����n ���㣬���������� ���㶼����ͬһ��ֱ����.����ÿ���㻭һ��ֱ�ߣ����ǿ��Էֱ�����ֱ�ߣ� �� ̽����Ϊ�˽��������⣬ϣ��С���ͬѧ����������±������̽������Ϊ�˷����� �����⣬ͼ��ÿ���߶α�ʾ���߶����˵��һ��ֱ�ߣ�
���㣬5 ���㣬����n ���㣬���������� ���㶼����ͬһ��ֱ����.����ÿ���㻭һ��ֱ�ߣ����ǿ��Էֱ�����ֱ�ߣ� �� ̽����Ϊ�˽��������⣬ϣ��С���ͬѧ����������±������̽������Ϊ�˷����� �����⣬ͼ��ÿ���߶α�ʾ���߶����˵��һ��ֱ�ߣ�
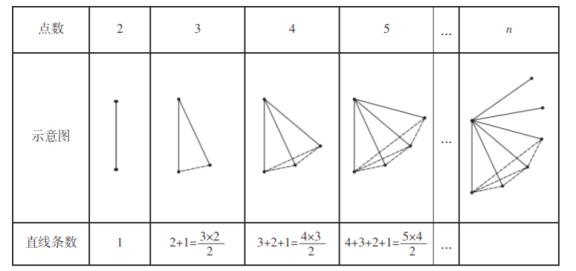
�����������⣺
��1�������ϣ��С����ɣ���ֱ��д�����ۣ���ƽ������![]() ����ʱ��ֱ������Ϊ ��
����ʱ��ֱ������Ϊ ��
��2����ijͬѧ���ձ����еķ�����������![]() ��ֱ�ߣ����ƽ�����ж��ٸ���֪��.
��ֱ�ߣ����ƽ�����ж��ٸ���֪��.
���𰸡���1��![]() ����2��8.
����2��8.
��������
��1�����ݹ������ֱ����1����������ͬһֱ���ϵ������ֱ����3�������κ����㶼����һ��ֱ�����ĵ��ֱ����6�������˹��ɣ������һ�㣬�ܽ����ʽ��![]() ����2����28���빫ʽ��n����.
����2����28���빫ʽ��n����.
�⣺��1����ƽ������2����ʱ�����Ի�![]() ��ֱ�ߣ�
��ֱ�ߣ�
��ƽ������3����ʱ�����Ի�![]() ��ֱ�ߣ�
��ֱ�ߣ�
��ƽ������4����ʱ�����Ի�![]() ��ֱ�ߣ�
��ֱ�ߣ�
��
��ƽ������n��n��2������ʱ�����Ի�![]() ��ֱ�ߣ�
��ֱ�ߣ�
![]() ���ƽ������
���ƽ������ ![]() ����֪��.
����֪��.
�����⣬��![]()
���![]() ���ᣩ
���ᣩ
�𣺸�ƽ������![]() ����֪��
����֪��

��ϰ��ϵ�д�
�����Ŀ