题目内容
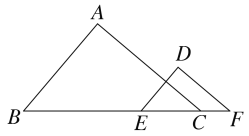
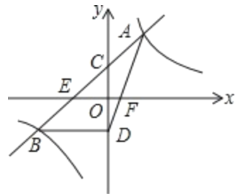
【题目】如图,反比例函数![]() 的图象与直线y=kx+b相交于点A、B,点A的坐标为(2,4),直线AB交y轴于点C(0,2),交x轴于点E.
的图象与直线y=kx+b相交于点A、B,点A的坐标为(2,4),直线AB交y轴于点C(0,2),交x轴于点E.
(1)求反比例函数与一次函数的表达式;
(2)求点E、B的坐标;
(3)过点B作BD⊥y轴,垂足为D,连接AD交x轴于点F,求![]() 的值.
的值.
【答案】(1)反比例函数表达式为![]() ,一次函数表达式为
,一次函数表达式为![]() ;(2)E (-2,0) ,B(-4,-2);(3)
;(2)E (-2,0) ,B(-4,-2);(3)![]()
【解析】
(1)采用待定系数法求反比例函数和一次函数表达式;
(2)求直线AC与x轴的交点,与反比例函数的交点即可得到E、B的坐标;
(3)由EF∥BD得到△AEF∽△ABD,利用坐标系中两点间的距离公式求出AE,AB得到相似比,利用面积比等于相似比的平方即可得到答案.
解:(1)∵反比例函数![]() 经过A (2,4),
经过A (2,4),
∴![]() ,解得
,解得![]() .
.
∴反比例函数表达式为![]()
∵直线y=kx+b经过A (2,4),C(0,2)
∴![]() ,解得
,解得![]() ,
,
∴一次函数表达式为![]()
(2)∵直线![]() 与x轴交于E点,当y=0时,
与x轴交于E点,当y=0时,![]() ,即
,即![]() ,
,
∴E点坐标为(-2,0)
将一次函数![]() 与反比例函数
与反比例函数![]() 联立得,
联立得,
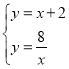 ,解得
,解得![]() 或
或![]()
∵A点坐标为(2,4)
∴B点坐标为(-4,-2)
(3)∵点A的坐标为(2,4),E点坐标为(-2,0),B点坐标为(-4,-2)
∴![]()
![]()
∴![]()
∵EF⊥y轴,BD⊥y轴
∴EF∥BD
∴△AEF∽△ABD
∴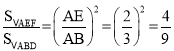

练习册系列答案
相关题目