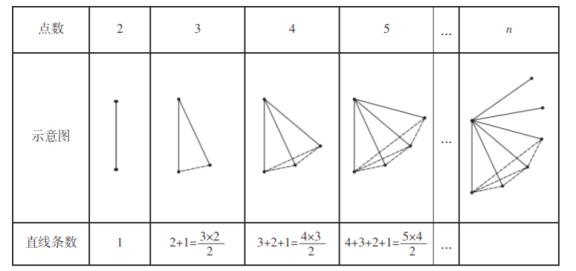
��Ŀ����
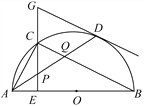
����Ŀ����ͼ1��������y��ax2��4ax+b������A��1��0������x�ύ�ڵ�B����y�ύ�ڵ�C����OB��OC��
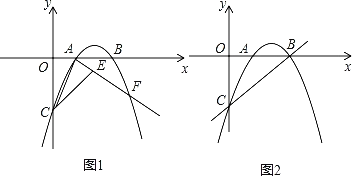
��1���������ߵĽ���ʽ��
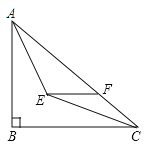
��2������OAC��AC���۵õ���ACE��ֱ��AE���������ڵ�P�����P�����ꣻ
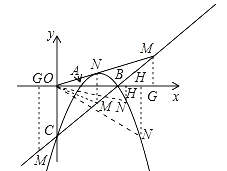
��3����ͼ2����MΪֱ��BC��һ�㣨����B��C�غϣ�����OM����OM��O����ת90�����õ��߶�ON���Ƿ���������ĵ�N��ʹ��Nǡ�����������ϣ������ڣ������N�����ꣻ�������ڣ�˵�����ɣ�
���𰸡���1��y����x2+4x��3����2����P��![]() ������3�����ڷ���������N�㣬������ΪN��2��1����5����8����
������3�����ڷ���������N�㣬������ΪN��2��1����5����8����
��������
��1�����������ߵĽ���ʽ���ɵ������ߵĶԳ��᷽�̣������ɸ��ݵ�A�������ʾ����B�����꣬��֪OB=OC�����ɵõ���C�����꣬�Ӷ����ô���ϵ������������ߵĽ���ʽ��
��2����PΪֱ��AE�������ߵĽ��㣬�����P�����������ֱ��AE�Ľ���ʽ����ֱ��AE��y��Ľ���ΪF������FOA�ס�FEC������OA=1��EC=3���������������εĶ�Ӧ�߳ɱ������ɵõ�FE=3OF����OF=x����EF=3x��AF=3x-1����������Rt��FOA�����x��ֵ��Ҳ�������F������꣬Ȼ�����ô���ϵ�������ֱ��AE�Ľ���ʽ�����������ߵĽ���ʽ���ɵõ���P�����꣮
��3������Ӧ������������ۣ�
�ٵ���M�ڵ�һ����ʱ������M��a��a-3��������ON����OM��ת90�����ã������OMN�ǵ���ֱ�������Σ��ֱ��M��N��MG��NH��ֱ��x�ᣬ����֤����OMG�ա�NOH����MG=OH��NH=OG���ɴ˿ɱ�ʾ��N������꣬Ȼ������������ߵĽ���ʽ�У�������õ�M��N�����ꣻ
�ڵ���M�ڵ������ޣ��ܵ�M�ڵ�������ʱ���ⷨͬ�٣�
��1��������֪�������ߵĶԳ���Ϊ��x=2����B��3��0����
��֪OB=OC=3����C��0��-3����
�������ߵĽ���ʽΪ��y=a��x-1����x-3�����������У�
a��0-1����0-3��=-3��a=-1��
�������ߵĽ���ʽΪ��y=-x2+4x-3��
��2����AE��y���ڵ�F��
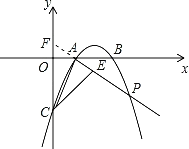
��֤����FOA�ס�FEC����![]() ��
��
��OF��x����EF��3x��
����FA��3x��1��
��Rt��FOA�У��ɹ��ɶ����ã�
��3x��1��2��x2+1��
���x��![]() ��
��
��OF��![]() ��F��0��
��F��0��![]() ����
����
���ֱ��AEΪy����![]() x+
x+![]() ��
��
���������ߵĽ���ʽ�ã�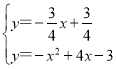 ��
��
��� ��
��![]() ��
��
�ʵ�P��![]() ��
��![]() ����
����
��3����B��3��0����C��0����3����
��ֱ��BC��y��x��3��
���M��a��a��3������
�ٵ���M�ڵ�һ����ʱ��OG��a��MG��a��3��
��M��MG��x����G����N��NH��x����H��
������ת������֪����MON��90����OM��ON��
���֤����MOG�ա�NOH���ã�
OG��NH��a��OH��MG��a��3��
��N��a��3����a����
������������ߵĽ���ʽ�У��ã�
����a��3��2+4��a��3����3����a��
�����ã�a2��11a+24��0��
a��3����ȥ����a��8��
��M��8��5����N��5����8����
�ڵ���M�ڵ�������ʱ��OG����a��MG��3��a��
ͬ�ٿɵã�MG��OH��3��a��OG��NH����a����N��3��a��a�������������ߵĽ���ʽ�ɵã�
����3��a��2+4��3��a����3��a��
�����ã�a2��a��0����a��0��a��1��
���ڵ�M�ڵ������ޣ�
����a��0��
��a��0��a��1���������⣬���������������
�۵���M�ڵ�������ʱ��OG��a��MG��3��a��
ͬ�ٵã�N��3��a��a�����ڢ����Ѿ���ô�ʱa��0����ȥ����a��1��
��M��1����2����N��2��1����
���Ͽ�֪�����ڷ���������N�㣬������ΪN��2��1����5����8����

 ��������������������ϵ�д�
��������������������ϵ�д�