题目内容
【题目】如图，已知一次函数y1＝x+m的图象与x轴y轴分别交于点A、B，与反比例函数y2＝
（x＜0）的图象分别交于点C、D，且C点的坐标为（﹣1，2）．
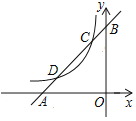
（1）分别求出一次函数及反比例函数的关系式；
（2）求出点D的坐标并直接写出y1＞y2的解集．
【答案】(1) 一次函数的解析式为y1＝x+3，反比例函数的解析式为：y2＝﹣
；（2）D（﹣2，1），y1＞y2的解集为﹣2＜x＜﹣1．
【解析】
（1）把点C（﹣1，2）分别代入一次函数y1=x+m，反比例函数y2=
，即可求出一次函数及反比例函数的关系式；
（2）联立解析式，解方程组即可求得D的坐标，然后根据图象即可求得y1＞y2为的解集．
（1）把点C（﹣1，2）代入y1=x+m得：2=﹣1+m，解得：m=3，把点C（﹣1，2）代入y2=（x＜0）得：2=
，解得：k2=﹣2，故一次函数的解析式为y1=x+3，反比例函数的解析式为：y2=﹣．
（2）解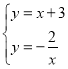
，得：
或
，∴D（﹣2，1），∴y1＞y2的解集为﹣2＜x＜﹣1．
【题目】某家电生产厂家去年销往农村的某品牌洗碗机每台的售价
（元）与月份
之间满足函数关系
，去年的月销售量户（万台）与月份之间成一次函数关系，其中两个月的销售情况如表：
月份： | 1月 | 5月 |
销售量： | 3.9万台 | 4.3万台 |
（1）求该品牌洗碗机在去年哪个月销往农村的销售金额最大？最大是多少？（提示：销售金额=销量×售价）
（2）经统计和计算.得到此洗碗机在农村地区的销售数据，如表：
销售数据信息表 | 售价（元/台） | 销量（万台） | 补贴金额（万元） |
去年12月份 | 2000 | 5 | / |
今年2月份 |
|
| / |
今年3月份 |
|
| 312 |
由于国家实施“家电下乡政策”，所以今年3月份国家按该产品售价的13%给子财政补贴，共补贴了312万元，从表格中，我们可以看出：今年3月份与今年2月份相比较，售价保持不变，但销量增加了1.5万台.今年2月份与去年12月份相比较，售价下降了
%，销量下降了1.5%；请用表示表格中的
，
，并根据已知条件求出的值.
