题目内容
【题目】已知直线 ![]() 与⊙O,AB是⊙O的直径,AD⊥
与⊙O,AB是⊙O的直径,AD⊥ ![]() 于点D.
于点D.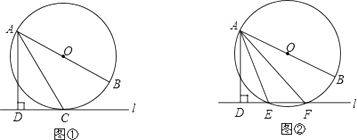
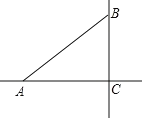
(1)如图①,当直线 ![]() 与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
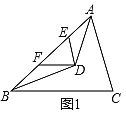
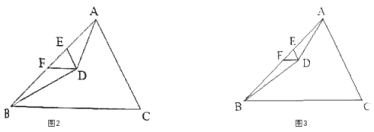
(2)如图②,当直线 ![]() 与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
【答案】
(1)解:连接OC、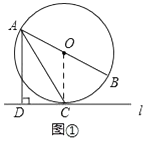
∵l是⊙O的切线,
∴OC⊥l,
∵AD⊥l,
∴OC∥AD,
∴∠OCA=∠DAC=30°,
∵OA=OC,
∴∠OAC=∠OCA=30°
(2)解:连接BE,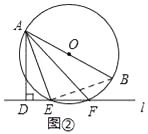
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠AED+∠BEF=90°,
∵∠AED+∠DAE=90°,
∴∠BEF=∠DAE=18°,
∵ ![]() ,
,
∴∠BAF=∠BEF=18°
【解析】(1)根据直线 l 与⊙O相切,连接OC,得出OC⊥l,再根据AD⊥l证得OC∥AD,然后根据平行线的性质及等腰三角形的性质,即可求出∠BAC的大小。
(2)连接BE,要求∠BAF的大小,根据圆周角定理只需求出∠BEF的度数,先证明∠BEF=∠DAE,再根据同弧所对的圆周角相等,即可求出∠BEF的度数。

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目