题目内容
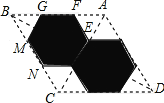
【题目】校园内有一个花坛,是由两个边长均为2.5m的正六边形围成的(如图中的阴影部分所示),学校现要将这个花坛在原有的基础上扩建成一个如图所示的菱形区域,则扩建后菱形区域的周长为( )

A.30mB.![]() mC.20mD.
mC.20mD.![]() m
m
【答案】A
【解析】
根据题意和正六边形的性质得出△BMG是等边三角形,再根据正六边形的边长得出BG=GM=2.5m,同理可证出AF=EF=2.5m,再根据AB=BG+GF+AF,求出AB,从而得出扩建后菱形区域的周长.
解:如图,∵花坛是由两个相同的正六边形围成,
∴∠FGM=∠GMN=120°,GM=GF=EF,
∴∠BMG=∠BGM=60°,
∴△BMG是等边三角形,
∴BG=GM=2.5(m),
同理可证:AF=EF=2.5(m)
∴AB=BG+GF+AF=2.5×3=7.5(m),
∴扩建后菱形区域的周长为7.5×4=30(m),
故选:A.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目