Question

【题目】如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“好玩三角形”，在Rt△ABC中，∠C=90°，若Rt△ABC是“好玩三角形”，则tanA= ．

Answer 1

【答案】 或
【解析】解：分两种情况：
①如图1，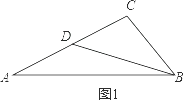

BD是AC边上的中线，BD=AC．
设AD=DC=k，则BD=AC=2k．
在Rt△BCD中，∵∠C=90°，
∴BC= = k，
∴tanA= = = ；
②如图2，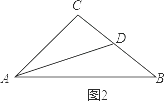

AD是BC边上的中线，AD=BC．
设BD=DC=k，则AD=BC=2k．
在Rt△ACD中，∵∠C=90°，
∴AC= = k，
∴tanB= = = ，
∵∠CAB+∠B=90°，
∴tan∠CAB= = = ．
综上可知，所求值为 或 ．
故答案为 或 ．
由“好玩三角形”的定义、勾股定理和正切的定义，得到tanA的值.