Question

【题目】(1)如图1，在△ABC中，AD、BD分别平分∠BAC和∠ABC，AD、BD相交于点D，过点D作DE∥AC，DF∥BC分别交AB于点E、F.

①若∠EDF=80°，则∠ADB=________°；

②若∠C=则∠ADB=________°.

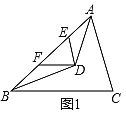
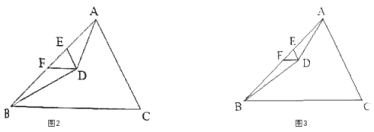
(2)如图2，在△ABC中，若∠BAD=∠BAC，∠ABD=∠ABC，AD、BD相交于点D，过点D作DE∥AC，DF∥BC分别交AB于点E、F，若∠EDF=60°，则∠ADB=_______°；

(3)如图3，在△ABC中，AD、BD分别是∠BAC、∠ABC的等分线，AD、BD相交于点D，若∠BAD=∠BAC，∠ABD=∠ABC，过点D作DE∥AC，DF∥BC分别交AB于点E、F，若∠EDF=，则∠ADB的度数是多少？(用表示)

Answer 1

【答案】（1）130°、（90-0.5x）（2）140°；（3）

【解析】

（1）①由∠EDF=80°及DE∥AC，DF∥BC，可求∠BAC+∠ABC =100°；再结合角平分线的定义及三角形的内角和即可求出∠ADB的值；②由角平分线的定义及三角形的内角和求解即可；

（2）参考（1）①的步骤求解即可；

（3）参考（2）的步骤求解即可.

（1）①∵∠EDF=80°，

∴∠DEF+∠DFE=100°.

∵DE∥AC，DF∥BC，

∴∠BAC=∠DEF，∠ABC=∠DFE，

∴∠BAC+∠ABC =100°.

∵AD、BD分别平分∠BAC和∠ABC，

∴∠BAD=∠BAC， ∠ABD=∠ABC，

∴∠BAD+∠ABD=(∠BAC+∠ABC)=50°，

∴∠ADC=180°-50°=130°；

②∵∠C=，

∴∠BAC+∠ABC =180°-，

∵AD、BD分别平分∠BAC和∠ABC，

∴∠BAD=∠BAC， ∠ABD=∠ABC，

∴∠BAD+∠ABD=(∠BAC+∠ABC)=(∠180°-)=（90-0.5x）°;

（2）∵∠EDF=60°，

∴∠DEF+∠DFE=120°.

∵DE∥AC，DF∥BC，

∴∠BAC=∠DEF，∠ABC=∠DFE，

∴∠BAC+∠ABC =120°.

∵∠BAD=∠BAC，∠ABD=∠ABC，

∴∠BAD+∠ABD= (∠BAC+∠ABC)=40°，

∴∠ADC=180°-40°=140°；

（3）∵∠EDF=，

∴∠DEF+∠DFE=120°.

∵DE∥AC，DF∥BC，

∴∠BAC=∠DEF，∠ABC=∠DFE，

∴∠BAC+∠ABC =（180-x）°.

∵BAD=∠BAC，∠ABD=∠ABC，

∴∠BAD+∠ABD= (180-x)°，

∴∠ADC=180°-.