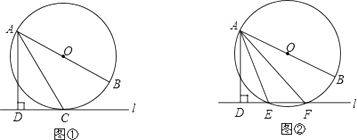题目内容
【题目】已知经过原点的抛物线 ![]() 与
与 ![]() 轴的另一个交点为
轴的另一个交点为 ![]() ,现将抛物线向右平移
,现将抛物线向右平移 ![]() 个单位长度,所得抛物线与
个单位长度,所得抛物线与 ![]() 轴交于
轴交于 ![]() ,与原抛物线交于点
,与原抛物线交于点 ![]() ,设
,设 ![]() 的面积为
的面积为 ![]() ,则用
,则用 ![]() 表示
表示 ![]() =
=
【答案】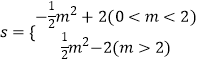
【解析】令-2x2+4x=0,得x1=0,x2=2
∴点A的坐标为(2,0),
如图1,当0<m<2时,作PH⊥x轴于H,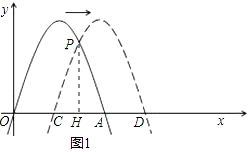
设P(xP , yP),
∵A(2,0),C(m,0)
∴AC=2-m,
∴CH= ![]()
∴xP=OH=m+ ![]()
把xP= ![]() 代入y=-2x2+4x,
代入y=-2x2+4x,
得yP=- ![]() m2+2
m2+2
∵CD=OA=2
∴S= ![]() CDHP=
CDHP= ![]() ×2×(-
×2×(- ![]() m2+2)=-
m2+2)=- ![]() m2+2
m2+2
如图2,当m>2时,作PH⊥x轴于H,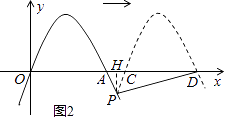
设P(xP , yP)
∵A(2,0),C(m,0)
∴AC=m-2,
∴AH= ![]()
∴xP=OH=2+ ![]() =
= ![]()
把xP= ![]() 代入y=-2x2+4x,得
代入y=-2x2+4x,得
yP=- ![]() m2+2
m2+2
∵CD=OA=2
∴S= ![]() CDHP=
CDHP= ![]() m2-2.
m2-2.
综上可得:s= 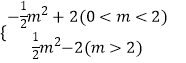 .
.
【考点精析】本题主要考查了抛物线与坐标轴的交点的相关知识点,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.

 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案【题目】某公司计划购买若干台打印机,现从两家商场了解到同一种型号的打印机报价均为1000元,并且多买都有一定的优惠.各商场的优惠条件如下表所示:
商场 | 优惠条件 |
甲商场 | 第一台按原价收费,其余的每台优惠15% |
乙商场 | 每台优惠10% |
(1)设公司购买![]() 台打印机,选择甲商场时,所需费用为
台打印机,选择甲商场时,所需费用为![]() 元,选择乙商场时,所需费用为
元,选择乙商场时,所需费用为![]() 元,请分别求出
元,请分别求出![]() ,
,![]() 与
与![]() 之间的关系式.
之间的关系式.
(2)什么情况下,两家商场的收费相同?什么情况下,到甲商场购买更优惠?什么情况下,到乙商场购买更优惠?
(3)现从甲乙两商场一共买入10台打印机,已知甲商场的运费为每台15元,乙商场的运费为每台20元,设总运费为![]() 元,从甲商场购买
元,从甲商场购买![]() 台打印机,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?
台打印机,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?