题目内容
【题目】如图,已知点P(2m-1,6m-5)在第一象限的角平分线OC 上,AP⊥BP,点A在x轴上,点 B在y 轴上.
(1)求点P 的坐标;
(2)当∠APB绕点P旋转时,OA+OB的值是否发生变化?若变化,求出其变化范围;若不变,求出这个定值.
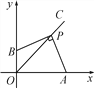
【答案】(1)点 P 的坐标为(1,1);(2) OA+OB 的值不发生变化,其值为 2.
【解析】试题分析:
(1)根据第一象限的角平分线上的点的横坐标与纵坐标相等列方程求解;
(2)作 PD⊥x 轴于点 D,PE⊥y 轴于点 E,证△PAD≌△PBE,可得OA+OB=2.
解:(1)由题意,得 2m-1=6m-5.解得 m=1,
∴点 P 的坐标为(1,1)
(2)作 PD⊥x 轴于点 D,PE⊥y 轴于点 E,
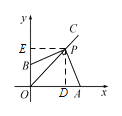
则△PAD≌△PBE,
∴AD=BE,
∴OA+OB=OD+AD+OB=OD+BE+OB=OD+OE=2,为定值,
故 OA+OB 的值不发生变化,其值为 2.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目