题目内容
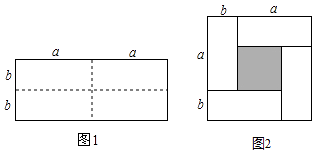
【题目】暑假期间,某学校计划用彩色的地面砖铺设教学楼门前一块矩形操场ABCD的地面.已知这个矩形操场地面的长为100m,宽为80m,图案设计如图所示:操场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,在实际铺设的过程总,阴影部分铺红色地面砖,其余部分铺灰色地面砖.
(1)如果操场上铺灰色地面砖的面积是铺红色地面砖面积的4倍,那么操场四角的每个小正方形边长是多少米?
(2)如果灰色地面砖的价格为每平方米30元,红色地面砖的价格为每平方米20元,学校现有15万元资金,问这些资金是否能购买所需的全部地面砖?如果能购买所学的全部地面砖,则剩余资金是多少元?如果不能购买所需的全部地面砖,教育局还应该至少给学校解决多少资金?

【答案】(1)操场四角的每个小正方形边长是5米;
(2)这些资金不能购买所需的全部地面砖,教育局还应该至少给学校解决19.95﹣15=4.95万元资金.
【解析】
试题分析:(1)设小正方形的边长为x米,表示出里边大矩形的长为(100﹣2x)米,宽为(80﹣2x)米,利用灰色部分的面积=4个小正方形的面积+里边大矩形的面积,红色部分面积=上下两个矩形面积+左右两个矩形面积,根据灰色地面砖的面积是铺红色地面砖面积的4倍列出关于x的方程,求出方程的解得到x的值,即为小正方形的边长;
(2)设铺矩形广场地面的总费用为y元,广场四角的小正方形的边长为x米,根据等量关系“总费用=铺白色地面砖的费用+铺绿色地面砖的费用”列出y关于x的函数,求得最小值,与15万元比较可得是否够用.
试题解析:(1)设操场四角的每个小正方形边长是x米,根据题意,
得:4x2+(100﹣2x)(80﹣2x)=4[2x(100﹣2x)+2x(80﹣2x)],
整理,得:x2﹣45x+200=0,
解得:x1=5,x2=40(舍去),
故操场四角的每个小正方形边长是5米;
(2)设铺矩形广场地面的总费用为y元,广场四角的小正方形的边长为x米,
则,y=30×[4x2+(100﹣2x)(80﹣2x)]+20×[2x(100﹣2x)+2x(80﹣2x)]
即:y=80x2﹣3600x+240000
配方得,y=80(x﹣22.5)2+199500
当x=22.5时,y的值最小,最小值为19.95万元>15万元,
故这些资金不能购买所需的全部地面砖,教育局还应该至少给学校解决19.95﹣15=4.95万元资金.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案