题目内容
【题目】求证:等腰三角形底边中线上任意一点到两腰的距离相等.
(1)在所给图形的基础上,根据题意画出图形.
(2)根据所画图形写出已知、求证.
(3)写出证明过程.

【答案】见解析
【解析】
试题根据题意画出图形,写出已知与求证,然后证明:由AB=AC,D为BC中点,利用等腰三角形的“三线合一”性质得到AD为顶角的平分线,根据角平分线上的点到角两边的距离相等即可得到PE=PF得证.
试题解析:
(1)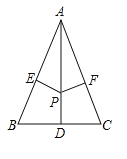
(2)已知:在![]() 中,AB=AC,AD是底边BC上的中线,点P是AD上任意一点,PE⊥AB垂足为点E,PF⊥AC垂足为点F
中,AB=AC,AD是底边BC上的中线,点P是AD上任意一点,PE⊥AB垂足为点E,PF⊥AC垂足为点F
求证:PE=PF
(3)![]() 在
在![]() 中,AB=AC,AD是底边BC上的中线
中,AB=AC,AD是底边BC上的中线
![]() ∠BAD=∠CAD
∠BAD=∠CAD
![]() PE⊥AB垂足为点E,PF⊥AC垂足为点F.
PE⊥AB垂足为点E,PF⊥AC垂足为点F.
![]() ∠AEP=∠AFP=90°
∠AEP=∠AFP=90°
在
![]()
![]() PE=PF
PE=PF

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目