题目内容
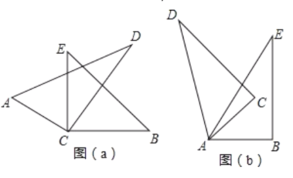
【题目】(1)如图(a),将一副三角尺(∠A=60°,∠B=45°)的直角顶点C叠放在一起,边CD与BE相交.
①若∠DCE=25°,则∠ACB=_____;若∠ACB=130°,则∠DCE= _____ ;
②猜想∠ACB与∠DCE的数量关系.直接写出答案,无需证明.
(2)如图(b),若两个相同的三角尺60°锐角的顶点A重合在一起, 边CD与A E相交,则∠DAB与∠CAE有何数量关系?请说明理由.
【答案】(1)①155°,50°,②∠ACB+∠DCE=180°;(2)∠DAB+∠CAE=120°,理由见解析
【解析】
(1)①先求出∠BCD,再代入∠ACB=∠ACD+∠BCD求出即可;先求出∠BCD,再代入∠DCE=∠BCE∠BCD求出即可;②根据∠ACB=∠ACE+∠DCE+∠DCE求出即可;
(2)根据∠DAB=∠DAE+∠CAE+∠CAB求出即可;
(1)①∵∠BCE=90°,∠DCE=25°,
∴∠BCD=∠BCE∠DCE=65°,
∵∠ACD=90°,
∴∠ACB=∠ACD+∠BCD=90°+65°=155°;
∵∠ACB=130°,∠ACD=90°,
∴∠BCD=∠ACB∠ACD=130°90°=40°,
∵∠BCE=90°,
∴∠DCE=∠BCE∠BCD=90°40°=50°,
故答案为:155°,50°;
②∠ACB+∠DCE=180°,
理由如下:∵∠ACB=∠ACE+∠DCE+∠DCE,
∴∠ACB+∠DCE
=∠ACE+∠DCE+∠DCE+∠DCE
=∠ACD+∠BCE
=180°;
(2)∠DAB+∠CAE=120°,理由如下:
∵∠DAB=∠DAE+∠CAE+∠CAB,
∴∠DAB+∠CAE
=∠DAE+∠CAE+∠CAB+∠CAE
=∠DAC+∠BAE
=120°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目