Question

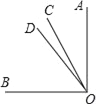
【题目】已知，点O是直线AB上一点，OC、OD为从点O引出的两条射线，∠BOD=30°，∠COD=∠AOC．

（1）如图①，求∠AOC的度数；

（2）如图②，在∠AOD的内部作∠MON=90°，请直接写出∠AON与∠COM之间的数量关系　 　；

（3）在（2）的条件下，若OM为∠BOC的角平分线，试说明∠AON=∠CON．

Answer 1

【答案】（1）∠AOC=70°；（2）∠AON+20°=∠COM；（3）详见解析.

【解析】

（1）由题意可知：∠AOD=∠AOC+∠COD，即∠AOC+∠AOC=150°，求解即可；

（2）由角的和差关系即可得出结论；

（3）OM是∠BOC的角平分线，可以求出∠CON=∠MON﹣∠COM=35°，而∠AON=∠AOC﹣∠CON=35°，即可得出结论．

（1）由题意可知：∠AOB=180°，∠BOD=30°，∠AOD=∠AOB﹣∠BOD=150°．

∵∠AOD=∠AOC+∠COD，∠COD=∠AOC，∴∠AOC+∠AOC=150°，∴∠AOC=70°；

（2）∵∠AOC=70°，∴∠AON+∠NOC=70°①．

∵∠MON=90°，∠MOC+∠NOC=90°②，由①②可得：∠AON+20°=∠COM；

（3）∵∠AOC=70°，∠AOB=180°，∴∠BOC=∠AOB﹣∠AOC=110°．

∵OM是∠BOC的角平分线，∴∠COM=∠BOC=55°．

∵∠MON=90°，∴∠CON=∠MON﹣∠COM=35°．

∵∠AOC=70°，∴∠AON=∠AOC﹣∠CON=35°，∴∠AON=∠CON．