题目内容
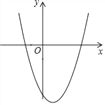
【题目】已知抛物线y=x2﹣x﹣6的图象如图所示.
(1)求抛物线与x轴、y轴的交点坐标;
(2)根据图象回答:当x取何值时,y>0?当x取何值时,y<0?
【答案】(1)与x轴的交点坐标为:(﹣2,0),(3,0),与y轴的交点坐标为:(0,﹣6);(2)见解析.
【解析】试题分析:(1)分别令x,y为零,求抛物线与坐标轴的交点.(2)利用(1)的结论,作图,观察可得,分别找函数图象在x轴上方和下方的部分所对的x的范围..
试题解析:
解:(1)令y=0,即x2﹣x﹣6=0,得,(x+2)(x﹣3)=0,
解此方程得:x1=﹣2,x2=3.
∴抛物线与x轴的交点坐标为:(﹣2,0),(3,0).
令x=0,得y=﹣6,
抛物线与y轴的交点坐标为:(0,﹣6).
(2)观察图象得:当x<﹣2或 x>3时,y>0;
当﹣2<x<3时,y<0.

【题目】某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
商品名称 | 甲 | 乙 |
进价 | 40 | 90 |
售价 | 60 | 120 |
设其中甲种商品购进x件,商场售完这100件商品的总利润为y元.
![]() 写出y关于x的函数关系式:
写出y关于x的函数关系式:
![]() 该商品计划最多投入8000元用于购买者两种商品,则至少要购进多少件甲商品?若销售完这些商品,则商场可获得的最大利润是多少元?
该商品计划最多投入8000元用于购买者两种商品,则至少要购进多少件甲商品?若销售完这些商品,则商场可获得的最大利润是多少元?
![]() 实际进货时,生产厂家对甲种商品的出厂价下调a元
实际进货时,生产厂家对甲种商品的出厂价下调a元![]() 出售
出售![]() 且限定商场最多购购进甲种商品60件,若商场保持同种商品的售价不变,请你根据以上信息及
且限定商场最多购购进甲种商品60件,若商场保持同种商品的售价不变,请你根据以上信息及![]() 中条件,设计出使该商场获得最大利润的进货方案.
中条件,设计出使该商场获得最大利润的进货方案.
【题目】“十一”期间,小聪跟爸爸一起去![]() 市旅游,出发前小聪从网上了解到
市旅游,出发前小聪从网上了解到![]() 市出租车收费标准如下:
市出租车收费标准如下:
行程(千米) |
| 满 |
|
收费标准(元) |
|
|
|
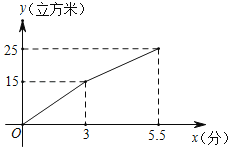
![]() 若甲、乙两地相距
若甲、乙两地相距![]() 千米,乘出租车从甲地到乙地需要付款多少元?
千米,乘出租车从甲地到乙地需要付款多少元?
![]() 小聪和爸爸从火车站乘出租车到旅馆,下车时计费表显示
小聪和爸爸从火车站乘出租车到旅馆,下车时计费表显示![]() 元,请你帮小聪算一算从火车站到旅馆的距离有多远?
元,请你帮小聪算一算从火车站到旅馆的距离有多远?
![]() 小聪的妈妈乘飞机来到
小聪的妈妈乘飞机来到![]() 市,小聪和爸爸从旅馆乘出租车到机场去接妈妈,到达机场时计费表显示
市,小聪和爸爸从旅馆乘出租车到机场去接妈妈,到达机场时计费表显示![]() 元,接完妈妈,立即沿原路返回旅馆(接人时间忽略不计),请帮小聪算一下乘原车返回和换乘另外的出租车,哪种更便宜?
元,接完妈妈,立即沿原路返回旅馆(接人时间忽略不计),请帮小聪算一下乘原车返回和换乘另外的出租车,哪种更便宜?