题目内容
【题目】如图,在![]() 中,AB=2AD,DE平分∠ADC,交AB于点E,交CB的延长线于点F,EG∥AD交DC于点G.
中,AB=2AD,DE平分∠ADC,交AB于点E,交CB的延长线于点F,EG∥AD交DC于点G.
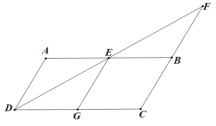
⑴求证:四边形AEGD为菱形;
⑵若![]() ,AD=2,求DF的长.
,AD=2,求DF的长.
【答案】(1)证明见解析;(2)4![]() .
.
【解析】
(1)先证出四边形AEGD是平行四边形,再由平行线的性质和角平分线证出∠ADE=∠AED,得出AD=AE,即可得出结论;
(2)连接AG交DF于H,由菱形的性质得出AD=DG,AG⊥DE,证出△ADG是等边三角形,AG=AD=2,得出∠ADH=30°,AH=![]() AG=1,由直角三角形的性质得出DH=
AG=1,由直角三角形的性质得出DH=![]() AH=
AH=![]() ,得出DE=2DH=2
,得出DE=2DH=2![]() ,证出DG=BE,由平行线的性质得出∠EDG=∠FEB,∠DGE=∠C=∠EBF,证明△DGE≌△EBF得出DE=EF,即可得出结果.
,证出DG=BE,由平行线的性质得出∠EDG=∠FEB,∠DGE=∠C=∠EBF,证明△DGE≌△EBF得出DE=EF,即可得出结果.
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠AED=∠GDE,
∵AE∥DG,EG∥AD,
∴四边形AEGD是平行四边形,
∵DE平分∠ADC,
∴∠ADE=∠GDE,
∴∠ADE=∠AED,
∴AD=AE,
∴四边形AEGD为菱形;
(2)解:连接AG交DF于H,如图所示:
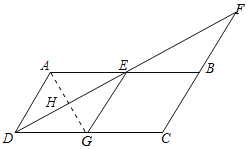
∵四边形AEGD为菱形,
∴AD=DG,AG⊥DE,
∵∠ADC=60°,AD=2,
∴△ADG是等边三角形,AG=AD=2,
∴∠ADH=30°,AH=![]() AG=1,
AG=1,
∴DH=![]() AH=
AH=![]() ,
,
∴DE=2DH=2![]() ,
,
∵AD=AE,AB=2AD,AD∥CF,EG∥AD,
∴DG=BE,∠EDG=∠FEB,∠DGE=∠C=∠EBF,
在△DGE和△EBF中,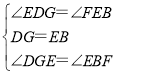
∴△DGE≌△EBF(ASA),
∴DE=EF,
∴DF=2DE=4![]() .
.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案【题目】某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为100分.前6名选手的得分如下:
序号 项目 | 1 | 2 | 3 | 4 | 5 | 6 |
笔试成绩/分 | 85 | 92 | 84 | 90 | 84 | 80 |
面试成绩/分 | 90 | 88 | 86 | 90 | 80 | 85 |
根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为100分).
(1)这6名选手笔试成绩的中位数是________分,众数是________分;
(2)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;
(3)求出其余五名选手的综合成绩,并以综合成绩排序确定前两名人选.
【题目】某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
商品名称 | 甲 | 乙 |
进价 | 40 | 90 |
售价 | 60 | 120 |
设其中甲种商品购进x件,商场售完这100件商品的总利润为y元.
![]() 写出y关于x的函数关系式:
写出y关于x的函数关系式:
![]() 该商品计划最多投入8000元用于购买者两种商品,则至少要购进多少件甲商品?若销售完这些商品,则商场可获得的最大利润是多少元?
该商品计划最多投入8000元用于购买者两种商品,则至少要购进多少件甲商品?若销售完这些商品,则商场可获得的最大利润是多少元?
![]() 实际进货时,生产厂家对甲种商品的出厂价下调a元
实际进货时,生产厂家对甲种商品的出厂价下调a元![]() 出售
出售![]() 且限定商场最多购购进甲种商品60件,若商场保持同种商品的售价不变,请你根据以上信息及
且限定商场最多购购进甲种商品60件,若商场保持同种商品的售价不变,请你根据以上信息及![]() 中条件,设计出使该商场获得最大利润的进货方案.
中条件,设计出使该商场获得最大利润的进货方案.