题目内容
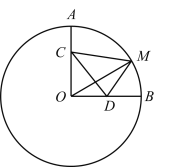
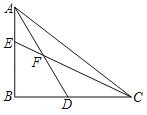
【题目】如图,![]() 中,
中,![]() ,以
,以![]() 的中点
的中点![]() 为圆心,以
为圆心,以![]() 的长为直径的
的长为直径的![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线
的切线![]() ,交
,交![]() 于点
于点![]() .
.
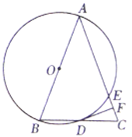
(1)求证:![]() ;
;
(2)填空:
①若![]() ,
,![]() ,则
,则![]() 的面积为____;
的面积为____;
②当![]() 的度数为____时,四边形
的度数为____时,四边形![]() 是菱形.
是菱形.
【答案】(1)见解析;(2)①![]() ;②30°
;②30°
【解析】
(1)由等腰三角形的性质得出∠B=∠C,∠B=∠BDO,证出OD∥AC,由已知条件得出∠C+∠CDF=90°,即可得出结论;
(2)解:①由AB是⊙O的直径,可得∠ADB=∠AEB=90°,即AD⊥BC由等腰三角形三线合一可得:BC=CD=![]() ,可证△ABE是等腰直角三角形,根据勾股定理可得:
,可证△ABE是等腰直角三角形,根据勾股定理可得:![]() ,代入数据可得:
,代入数据可得:![]() 故
故![]() 可得△BEC的面积,证得:△CBE∽△CDF,故
可得△BEC的面积,证得:△CBE∽△CDF,故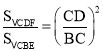 ,即可得出答案;
,即可得出答案;
②证出△ABC是等边三角形,得出∠ACB=60°,故∠CDF的度数,即可得出答案.
(1)证明:连接OD,∵AB=AC,OB=OD,
∴∠B=∠C,∠B=∠BDO,
∴∠C=∠BDO,
∴OD∥AC,
∵DF是⊙O的切线,
∴∠ODF=90°,
∴∠BDO+∠CDF=90°,
∴∠C+∠CDF=90°,
∴∠CFD=90°,
∴DF⊥AC;
(2)解:①∵连接AC,BE,
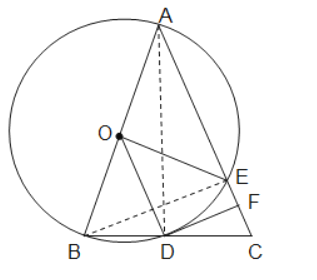
∵AB是⊙O的直径,
∴∠ADB=∠AEB=90°,
∴AD⊥BC
∵AB=AD=4,
∴BC=CD=![]() ,
,
在Rt△ABE中,∠AEB=90°,∠BAE=45°
∴∠ABE=90°-∠BAE=45°=∠BAE,
∴BE=AE
根据勾股定理可得![]() ,
,
即![]()
∴![]()
∴![]()
∴![]()
∴![]()
∵DF⊥AC
∴∠DFE=∠DFC=90°
∵∠AEB=90°
∴∠AEB=∠DFE
∴BE∥DF,
∴△CBE∽△CDF
∴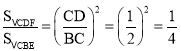
∴![]()
故答案为:![]()
②当四边形OECD是菱形时,OE∥DC
∴∠OEA=∠ACB
∵AB=AC,OA=OE
∴∠ABC=∠ACB,∠OAE=∠OEA
∴∠OAE=∠ABC=∠ACB
∴△ABC是等边三角形
∴∠ACB=60°
∴∠CDF=90°-∠DCF=90°-60°=30°
∴当∠CDF得度数为30°,四边形OECD是菱形
故答案为30°

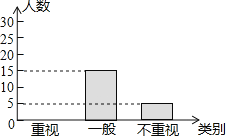
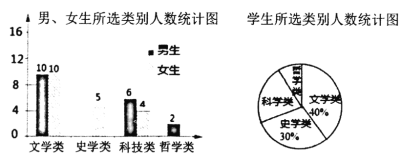
【题目】某教研机构为了了解初中生课外阅读名著的现状,随机抽取了某校50名初中生进行调查,依据相关数据绘制成了以下不完整的统计图,请根据图中信息解答下列问题:
类别 | 重视 | 一般 | 不重视 |
人数 | a | 15 | b |
(1)求表格中a,b的值;
(2)请补全统计图;
(3)若某校共有初中生2000名,请估计该校“重视课外阅读名著”的初中生人数.