ĢāÄæÄŚČŻ
”¾ĢāÄæ”æ4ŌĀ23ČÕŹĒŹĄ½ē¶ĮŹéČÕ£¬ÉčĮ¢µÄÄæµÄŹĒĶʶÆøü¶ąµÄČĖČ„ŌĶĮŗĶŠ“×÷£®ĪŖĮĖ½āѧɜµÄæĪĶāŌĶĮĒéæö£¬¶ŌijŠ£°ĖÄź¼¶1°ą”°Äć×īĻ²°®µÄæĪĶāŌĶĮŹéÄæ”±½ųŠŠµ÷²é£ØĆæĆūѧɜ±ŲŠėŃ”Ņ»ĄąĒŅÖ»ÄÜŃ”Ņ»ĄąŌĶĮŹéÄ棩£¬²¢øł¾Żµ÷²é½į¹ū»ęÖĘ³ÉČēĶ¼ĖłŹ¾µÄĮ½·łĶ³¼ĘĶ¼£Ø²»ĶźÕū£©£®
øł¾ŻŅŌÉĻŠÅĻ¢½ā¾öĻĀĮŠĪŹĢā
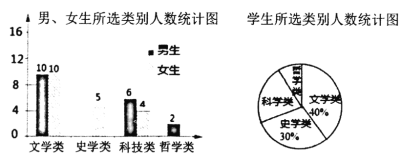
£Ø1£©Ėł³é²éµÄѧɜ֊£¬Ń”Ź·Ń§ĄąµÄÄŠÉśÓŠ______ČĖ£¬Ń”ÕÜѧĄąµÄÅ®ÉśÓŠ______ČĖ£»
£Ø2£©ÉČŠĪĶ³¼ĘĶ¼ÖŠ”°æĘѧĄą”±Ėł¶ŌÓ¦ÉČŠĪŌ²ŠÄ½Ē¶ČŹżĪŖ_______”ć£»
£Ø3£©ČōøĆŠ£ÓŠ2000Ćūѧɜ£¬Ēė¹Ą¼ĘøĆŠ£Ļ²°®”°æĘѧĄą”±µÄѧɜ¹²ÓŠ¶ąÉŁČĖ£æ
£Ø4£©“ÓĖł³éČ”µÄŃ””°ÕÜѧĄą”±µÄѧɜ֊£¬Ė껜єȔĮ½Ćūѧɜ²Ī¼ÓĒų¼¶±ēĀŪČü£¬ĒėÓĆŹ÷דĶ¼»ņĮŠ±ķ·ØĒó³öĖłŃ”Č”µÄĮ½ĆūѧɜĒ”ŗĆє֊Ņ»øöÄŠÉś”¢Ņ»øöÅ®ÉśµÄøÅĀŹ£®
”¾“š°ø”æ£Ø1£©10£»3£»£Ø2£©72£»£Ø3£©![]() £Ø4£©±ķøń¼ū½āĪö£»
£Ø4£©±ķøń¼ū½āĪö£»![]()
”¾½āĪö”æ
£Ø1£©ĄūÓĆŃ”ĪÄѧĄąµÄČĖŹż³żŅŌĘäĖłÕ¼µ÷²éČĖŹżµÄ°Ł·Ö±Č¼“æÉĒó³öµ÷²éČĖŹż£¬Č»ŗóĄūÓƵ÷²éČĖŹż³ĖŅŌ30%¼“æÉĒó³öŃ”Ź·Ń§ĄąµÄČĖŹż£¬“Ó¶ų¼ĘĖć³öŃ”Ź·Ń§ĄąµÄÄŠÉśČĖŹż£¬ŌŁĄūÓƵ÷²éČĖŹż¼õČ„ĘäÓąø÷ĄąČĖŹż¼“æÉĒó³öŃ”ÕÜѧĄąµÄÅ®ÉśČĖŹż£»
£Ø2£©ĄūÓĆŃ”æĘѧĄąČĖŹż³żŅŌµ÷²é×ÜČĖŹżŌŁ³Ė360”ć¼“æÉĒó³ö½įĀŪ£»
£Ø3£©ĄūÓĆŃ”æĘѧĄąČĖŹż³żŅŌµ÷²é×ÜČĖŹżŌŁ³Ė2000¼“æÉĒó³ö½įĀŪ£»
£Ø4£©øł¾ŻĢāŅā£¬ĮŠ³ö±ķøń£¬Č»ŗóĄūÓĆøÅĀŹ¹«Ź½ĒóøÅĀŹ¼“æÉ£®
½ā£ŗ£Ø1£©µ÷²é×ÜČĖŹżĪŖ£Ø10£«10£©”Ā40%=50ČĖ
Ń”Ź·Ń§ĄąµÄÄŠÉśÓŠ50”Į30%£5=10ČĖ
Ń”ÕÜѧĄąµÄÅ®ÉśÓŠ50£10£10£10£5£6£4£2=3ČĖ
¹Ź“š°øĪŖ£ŗ10£»3£»
£Ø2£©£Ø6£«4£©”Ā50”Į360”ć=72”ć
¹Ź“š°øĪŖ72£»
£Ø3£©![]()
![]() £ØČĖ£©
£ØČĖ£©
“š£ŗ¹Ą¼ĘøĆŠ£Ļ²°®”°æĘѧĄą”±µÄѧɜ¹²ÓŠ400ČĖ£»
£Ø4£©ĮŠ±ķČēĻĀ£ŗ
Ċ1 | Ċ2 | Ů1 | Ů2 | Ů3 | |
ÄŠ1 | ÄŠ2£¬ÄŠ1 | Å®1£¬ÄŠ1 | Å®2£¬ÄŠ1 | Å®3£¬ÄŠ1 | |
ÄŠ2 | ÄŠ1£¬ÄŠ2 | Å®1£¬ÄŠ2 | Å®2£¬ÄŠ2 | Å®3£¬ÄŠ2 | |
Å®1 | ÄŠ1£¬Å®1 | ÄŠ2£¬Å®1 | Å®2£¬Å®/span>1 | Å®3£¬Å®1 | |
Å®2 | ÄŠ1£¬Å®2 | ÄŠ2£¬Å®2 | Å®1£¬Å®2 | Å®3£¬Å®2 | |
Å®3 | ÄŠ1£¬Å®3 | ÄŠ2£¬Å®3 | Å®1£¬Å®3 | Å®2£¬Å®3 |
ÓɱķøńæÉÖŖ£ŗ¹²ÓŠ20ÖÖµČæÉÄܵĽį¹ū£¬ĘäÖŠĖłŃ”Č”µÄĮ½ĆūѧɜĒ”ŗĆє֊Ņ»øöÄŠÉś”¢Ņ»øöÅ®ÉśµÄæÉÄÜÓŠ12ÖÖ£¬
![]()
“š£ŗĖłŃ”Č”µÄĮ½ĆūѧɜĒ”ŗĆє֊Ņ»øöÄŠÉś”¢Ņ»øöÅ®ÉśµÄøÅĀŹĪŖ![]() £®
£®

 ŌĶĮæģ³µĻµĮŠ“š°ø
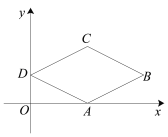
ŌĶĮæģ³µĻµĮŠ“š°ø”¾ĢāÄæ”æĻĀ±ķÖŠøų³ö![]() £¬
£¬![]() £¬
£¬![]() ČżÖÖŹÖ»śĶØ»°µÄŹÕ·Ń·½Ź½£®
ČżÖÖŹÖ»śĶØ»°µÄŹÕ·Ń·½Ź½£®
ŹÕ·Ń·½Ź½ | ŌĀĶØ»°·Ń/ŌŖ | °üŹ±ĶØ»°Ź±¼ä/ | ³¬Ź±·Ń/£ØŌŖ/ |
|
|
|
|
|
|
|
|
|
| ²»ĻŽŹ± |
£Ø1£©ÉčŌĀĶØ»°Ź±¼äĪŖ![]() Š”Ź±£¬Ōņ·½°ø
Š”Ź±£¬Ōņ·½°ø![]() £¬
£¬![]() £¬
£¬![]() µÄŹÕ·Ń½š¶ī
µÄŹÕ·Ń½š¶ī![]() £¬
£¬![]() £¬
£¬![]() ¶¼ŹĒ
¶¼ŹĒ![]() µÄŗÆŹż£¬Ēė·Ö±šĒó³öÕāČżøöŗÆŹż½āĪöŹ½£®
µÄŗÆŹż£¬Ēė·Ö±šĒó³öÕāČżøöŗÆŹż½āĪöŹ½£®
£Ø2£©ĢīæÕ£ŗ
ČōŃ”Ōń·½Ź½![]() ×īŹ”Ē®£¬ŌņŌĀĶØ»°Ź±¼ä
×īŹ”Ē®£¬ŌņŌĀĶØ»°Ź±¼ä![]() µÄȔֵ·¶Ī§ĪŖ______£»
µÄȔֵ·¶Ī§ĪŖ______£»
ČōŃ”Ōń·½Ź½![]() ×īŹ”Ē®£¬ŌņŌĀĶØ»°Ź±¼ä
×īŹ”Ē®£¬ŌņŌĀĶØ»°Ź±¼ä![]() µÄȔֵ·¶Ī§ĪŖ______£»
µÄȔֵ·¶Ī§ĪŖ______£»
ČōŃ”Ōń·½Ź½![]() ×īŹ”Ē®£¬ŌņŌĀĶØ»°Ź±¼ä
×īŹ”Ē®£¬ŌņŌĀĶØ»°Ź±¼ä![]() µÄȔֵ·¶Ī§ĪŖ______£»
µÄȔֵ·¶Ī§ĪŖ______£»
£Ø3£©Š”Ķõ”¢Š”ÕŽńÄź![]() ŌĀ·ŻĶØ»°·Ń¾łĪŖ
ŌĀ·ŻĶØ»°·Ń¾łĪŖ![]() ŌŖ£¬µ«Š”Ķõ±ČŠ”ÕÅĶØ»°Ź±¼ä³¤£¬ĒóŠ”ĶõøĆŌĀµÄĶØ»°Ź±¼ä£®
ŌŖ£¬µ«Š”Ķõ±ČŠ”ÕÅĶØ»°Ź±¼ä³¤£¬ĒóŠ”ĶõøĆŌĀµÄĶØ»°Ź±¼ä£®