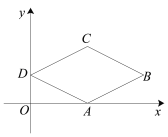
题目内容
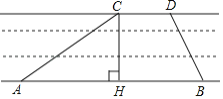
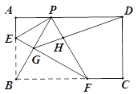
【题目】如图在矩形ABCD中，AB=6，AD=
，点E在AB上，且AE=2，将该矩形沿EF折叠，使点B恰好落在AD边上的点P处，连接PB交EF于点G，连接PF、DG它们的交点为点H，则HD=______．
【答案】
【解析】
构造以DG为斜边的直角三角形，利用勾股定理算出DG的长度，再利用相似算出DH的长度即可．
解：分别取AP中点N，连接DF、NG
则
，
∵折叠
∴EP=BE=4，BG=PG，BF=PF
又∵N是AP的中点
∴
， 
，
∴
∵AB=6，AE=2
∴BE=6-2=4
在Rt△AEP中，∠A=90°，AE=2，EP=4
∴由勾股定理可得：
∴
∴
∴
∴
∵
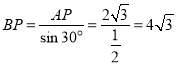
，N是AP的中点
∴
， 
∴
在Rt△DNG中，∠DNG=90°，
，
∴由勾股定理可得：
∵，
∴
又∵BF=PF
∴△BFP是等边三角形
∴BF=BP=
∴BF=PD
又∵BF∥PD
∴四边形BFDP是平行四边形
∴BP∥FD，BP=FD
所以
，
∴△HGP∽△HDF
∴
∴
练习册系列答案
相关题目
