题目内容
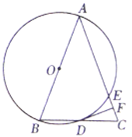
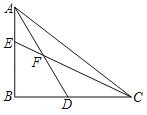
【题目】如图,在△ABC中,∠ABC=90°,D为BC的中点,点E在AB上,AD,CE交于点F,AE=EF=4,FC=9,则cos∠ACB的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
如图,延长AD到M,使得DM=DF,连接BM.利用全等三角形的性质证明BM=CF=9,AB=BM,利用勾股定理求出BC,AC即可解决问题.
解:如图,延长AD到M,使得DM=DF,连接BM.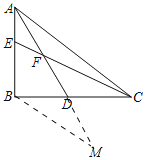
∵BD=DC,∠BDM=∠CDF,DM=DF,
∴△BDM≌△CDF(SAS),
∴CF=BM=9,∠M=∠CFD,
∵CE∥BM,
∴∠AFE=∠M,
∵EA=EF,
∴∠EAF=∠EFA,
∴∠BAM=∠M,
∴AB=BM=9,
∵AE=4,
∴BE=5,
∵∠EBC=90°,
∴BC=![]() =12,
=12,
∴AC=![]() =15,
=15,
∴cos∠ACB=![]() ,
,
故选:D.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目