题目内容
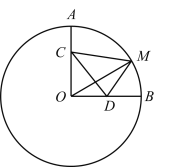
【题目】如图,在⊙O中,点A、点B在⊙O上,∠AOB=90°,OA=6,点C在OA上,且OC=2AC,点D是OB的中点,点M是劣弧AB上的动点,则CM+2DM的最小值为_______.
【答案】![]()
【解析】
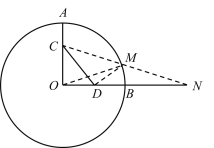
延长OB至点N,使得OB=BN,连接CN,CN与圆O交于M,证明△MOD∽△NOM,得到2DM= MN,将CM+2DM的最小值转化为为CM+MN,即CN,再利用勾股定理求解即可.
解:延长OB至点N,使得OB=BN,连接CN,CN与圆O交于M,
∵∠AOB=90°,OA=6,OC=2AC,点D是OB的中点,
∴AC=2,OC=4,OD=BD=3,OB=BN=6,
∵∠MOD=∠NOM,![]() ,
,
∴△MOD∽△NOM,
∴DM:MN=1:2,即2DM= MN,
∴CM+2DM的最小值为CM+MN,即CN,
在△CNO中,ON=12,OC=4,
∴CN=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目