题目内容
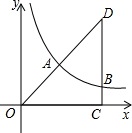
已知边长为4的正方形ABCD,顶点A与坐标原点重合,一反比例函数图象过顶点C,动点P以每秒1个单位速度从点A出发沿AB方向运动,动点Q同时以每秒4个单位速度从D点出发沿正方形的边DC-CB-BA方向顺时针折线运动,当点P与点Q相遇时停止运动,设点P的运动时间为t.
(1)求出该反比例函数解析式.
(2)连接PD,当以点Q和正方形的某两个顶点组成的三角形和△PAD全等时,求点Q的坐标.
(3)用含t的代数式表示以点Q、P、D为顶点的三角形的面积S,并指出相应t的取值范围.

(1)求出该反比例函数解析式.
(2)连接PD,当以点Q和正方形的某两个顶点组成的三角形和△PAD全等时,求点Q的坐标.
(3)用含t的代数式表示以点Q、P、D为顶点的三角形的面积S,并指出相应t的取值范围.

(1)∵正方形ABCD的边长为4,
∴C的坐标为(4,4),
设反比例解析式为y=
,
将C的坐标代入解析式得:k=16,
则反比例解析式为y=
;
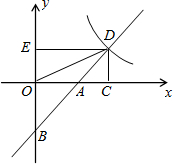
(2)当Q在DC上时,如图所示:
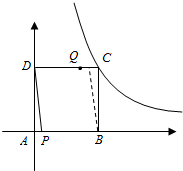
此时△APD≌△CQB,
∴AP=CQ,即t=4-4t,解得t=
,
则DQ=4t=
,即Q1(
,4);
当Q在BC边上时,有两个位置,如图所示:
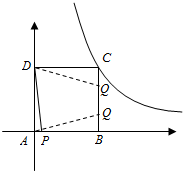
若Q在上边,则△QCD≌△PAD,
∴AP=QC,即4t-4=t,解得t=
,
则QB=8-4t=
,此时Q2(4,
);
若Q在下边,则△APD≌△BQA,
则AP=BQ,即8-4t=t,解得t=
,
则QB=
,即Q3(4,
);
当Q在AB边上时,如图所示:
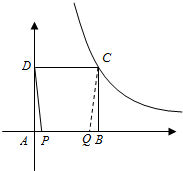
此时△APD≌△QBC,
∴AP=BQ,即4t-8=t,解得t=
,
因为0≤t≤
,所以舍去.
当t=2.4时,P、Q在AB上重合,此时△ADP和△QAD重合,重合时两三角形肯定全等,
∴Q4(2.4,0)
综上,Q1(
,4);Q2(4,
);Q3(4,
),Q4(2.4,0)
;
(3)S1=8t(0<t≤1);S2=-2t2+2t+8(1≤t≤2);S3=-10t+24(2≤t≤
).
∴C的坐标为(4,4),
设反比例解析式为y=
| k |
| x |
将C的坐标代入解析式得:k=16,
则反比例解析式为y=
| 16 |
| x |
(2)当Q在DC上时,如图所示:

此时△APD≌△CQB,
∴AP=CQ,即t=4-4t,解得t=
| 4 |
| 5 |
则DQ=4t=
| 16 |
| 5 |
| 16 |
| 5 |
当Q在BC边上时,有两个位置,如图所示:

若Q在上边,则△QCD≌△PAD,
∴AP=QC,即4t-4=t,解得t=
| 4 |
| 3 |
则QB=8-4t=
| 8 |
| 3 |
| 8 |
| 3 |
若Q在下边,则△APD≌△BQA,
则AP=BQ,即8-4t=t,解得t=
| 8 |
| 5 |
则QB=
| 8 |
| 5 |
| 8 |
| 5 |
当Q在AB边上时,如图所示:

此时△APD≌△QBC,
∴AP=BQ,即4t-8=t,解得t=
| 8 |
| 3 |
因为0≤t≤
| 12 |
| 5 |
当t=2.4时,P、Q在AB上重合,此时△ADP和△QAD重合,重合时两三角形肯定全等,
∴Q4(2.4,0)
综上,Q1(
| 16 |
| 5 |
| 8 |
| 3 |
| 8 |
| 5 |
;
(3)S1=8t(0<t≤1);S2=-2t2+2t+8(1≤t≤2);S3=-10t+24(2≤t≤
| 12 |
| 5 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目