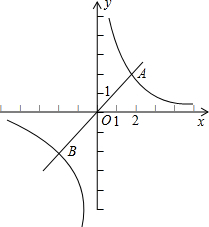题目内容
如图1,直线y=-x+4与x轴交于点B,与y轴交于点C,交双曲线y=
(x<0)于点N,连ON,且S△OBN=10.
(1)求双曲线的解析式;
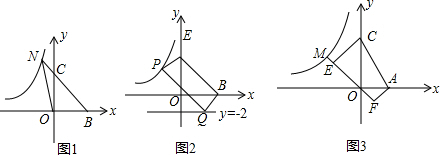
(2)如图2,平移直线BC交双曲线于点P,交直线y=-2于点Q,∠FCB=∠QBC,PC=QB求平移后的直线PQ的解析式;
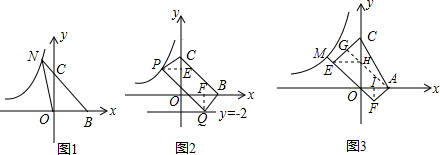
(3)如图3,已知A(2,0)点M为双曲线上一点,CE⊥OM于M,AF⊥OM于F,设梯形CEFA的面积为S,且AF•EF=
S,求点M的坐标.
| k |
| x |

(1)求双曲线的解析式;
(2)如图2,平移直线BC交双曲线于点P,交直线y=-2于点Q,∠FCB=∠QBC,PC=QB求平移后的直线PQ的解析式;
(3)如图3,已知A(2,0)点M为双曲线上一点,CE⊥OM于M,AF⊥OM于F,设梯形CEFA的面积为S,且AF•EF=
| 2 |
| 3 |
(1)∵当y=0时,即-x+4=0,
解得:x=4,
当x=0时,y=4,
∴点B的坐标为:(4,0),点C的坐标为(0,4),
∴OB=OC=4,
∵S△OBN=10,
∴S△OBN=S△OCN+S△OBC=10,
设点N的坐标为(x,y),
∴
×4×|x|+
×4×4=10,
∴x=-1,
∴y=-x+4=1+4=5,
∴点N的坐标为:(-1,5),
∴k=xy=-5,
∴双曲线的解析式为:y=-
;
(2)作PE⊥y轴于E,作QF⊥x轴于F,
则∠PEC=∠QFB=90°,
∵OB=OC,
∴∠OCB=∠OBC,
∵∠PCB=∠QBC,
∴∠PCE=∠QBF,
在△PCE和△QBC中,
,
∴△PCE≌△QBF(AAS),
∴PE=QF=2,
令x=-2,则y=-
=
,
∴P点的坐标为:(-2,
),
∵PQ∥BC,
∴设直线PQ的解析式为:y=-x+b,
将P(-2,
)代入得:
=2+b,
解得:b=
,
∴平移后的直线PQ的解析式为:y=-x+
;
(3)作AG⊥EC于G,交OC于H,作FI⊥OA于I,连接EH,
∵CE⊥EF,FA⊥EF,
∴四边形AFEG是矩形,
∴∠GAF=90°,EG=FA,
∵S=
(AF+EC)•EF,AF•EF=
S,
∴AF•EF=
(AF•EF+EC•EF),
∴EC=2AF,
∴EG=
EC,
即EG=GC,
∵GH⊥EC,
∴CH=EH,
∴∠CEH=∠ECH,
∵∠HEO+∠CEH=∠EOH+∠ECH=90°,
∴∠HEO=∠EOH,
∴EH=OH=
OC=2,
∵OA=2,
∴OH=OA,
∴∠HAO=45°,
∴∠OAF=45°,
∴OI=OF=1,
∴点F的坐标为(1,-1),
设直线EF的解析式为:y=kx,
∴k=-1,
∴直线EF的解析式为:y=-x,
联立:
,
解得:
(舍去),
.
∴点M的坐标为:(-
,
).
解得:x=4,
当x=0时,y=4,
∴点B的坐标为:(4,0),点C的坐标为(0,4),
∴OB=OC=4,
∵S△OBN=10,
∴S△OBN=S△OCN+S△OBC=10,
设点N的坐标为(x,y),
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴x=-1,
∴y=-x+4=1+4=5,
∴点N的坐标为:(-1,5),
∴k=xy=-5,
∴双曲线的解析式为:y=-
| 5 |
| x |
(2)作PE⊥y轴于E,作QF⊥x轴于F,
则∠PEC=∠QFB=90°,
∵OB=OC,
∴∠OCB=∠OBC,
∵∠PCB=∠QBC,
∴∠PCE=∠QBF,
在△PCE和△QBC中,
|
∴△PCE≌△QBF(AAS),
∴PE=QF=2,
令x=-2,则y=-
| 5 |
| -2 |
| 5 |
| 2 |
∴P点的坐标为:(-2,
| 5 |
| 2 |
∵PQ∥BC,
∴设直线PQ的解析式为:y=-x+b,
将P(-2,
| 5 |
| 2 |
| 5 |
| 2 |
解得:b=
| 1 |
| 2 |
∴平移后的直线PQ的解析式为:y=-x+
| 1 |
| 2 |
(3)作AG⊥EC于G,交OC于H,作FI⊥OA于I,连接EH,
∵CE⊥EF,FA⊥EF,
∴四边形AFEG是矩形,
∴∠GAF=90°,EG=FA,
∵S=
| 1 |
| 2 |
| 2 |
| 3 |
∴AF•EF=
| 1 |
| 3 |
∴EC=2AF,
∴EG=
| 1 |
| 2 |
即EG=GC,
∵GH⊥EC,
∴CH=EH,
∴∠CEH=∠ECH,
∵∠HEO+∠CEH=∠EOH+∠ECH=90°,
∴∠HEO=∠EOH,
∴EH=OH=
| 1 |
| 2 |
∵OA=2,
∴OH=OA,
∴∠HAO=45°,
∴∠OAF=45°,
∴OI=OF=1,
∴点F的坐标为(1,-1),
设直线EF的解析式为:y=kx,
∴k=-1,
∴直线EF的解析式为:y=-x,
联立:
|
解得:
|
|
∴点M的坐标为:(-
| 5 |
| 5 |


练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目